Подготовка к ОГЭ. Разборка 26 задания.

Подготовка к ОГЭ Задание 26.

Автор:

Учитель математики МБОУ «Лукашевская СОШ»

Преснова Анастасия Андреевна

Точки M и N лежат на диагонали АС ромба ABCD на расстоянии соответственно

3 и 6 от точки А. Найдите радиус окружности, проходящей через точку M и N и

касающийся стороны AB, если cos  DAC =

B

L

О

А

C

M

N

D

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 30.09.2014

Вспомогательные задачи

Окружность с центром на стороне AC треугольника ABC проходит через точку C

и касается прямой AB в точке B.Найдите AB, если диаметр окружности равен 15,

а AF =1.F точка пересечения окружности со стороной треугольника.

Решение:

По теореме о касательной

и секущей:

AB 2 = AC*AF

AC = AF+FC=16

AB =  16

AB = 4

Найти:

Дано:

AB - ?

FC=15

AF=1

AB-касательная

B

C

A

F

Ответ: AB = 4

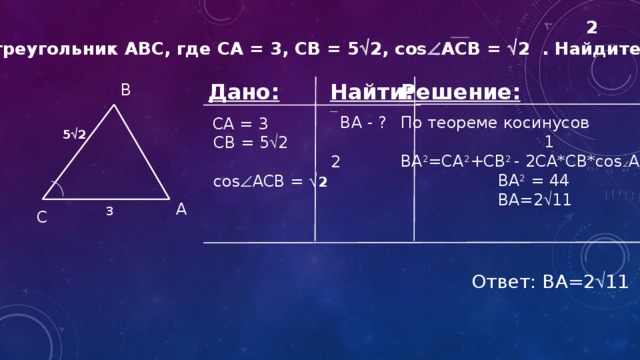
2

Дан треугольник ABC, где CA = 3, CB = 5  2, cos  ACB =  2 . Найдите BA.

Решение:

Найти:

Дано:

CA = 3

По теореме косинусов

BA - ?

CB = 5  2

1

2

BA 2 =CA 2 +CB 2 - 2CA*CB*cos  ABC

BA 2 = 44

cos  ACB =  2

BA=2  11

B

5  2

A

3

С

Ответ: BA=2  11

Хорда AB стягивает дугу окружности в 82  . Найдите угол ABC между этой хордой

и касательной к окружности, проведенной через точку B. Найдите  AOB, где

О-центр данной окружности. (Углы представьте как в градусах так и через дуги.)

B

Найти:

 ABC - ?

 AOB - ?

Решение:

 AOB – центральный угол

 AOB=82  

 AOB = BA

Рассмотрим  AOB. AO=OB=R

 AOB-равнобедренный

 OBA=  BAO =(180  -82  )/2=49 

По свойству радиуса, проведенного

в точку касания угол OBC=90 

 ABC= 90  - 49  = 41 

По свойству углов связанных с

окружностью 

 ABC =1/2 BA

Дано:

BA-хорда

BC-касательная



AB =82 

C

A

O

Ответ: 

 ABC =1/2 BA = 41 



 AOB = BA= 82 

Основная задача

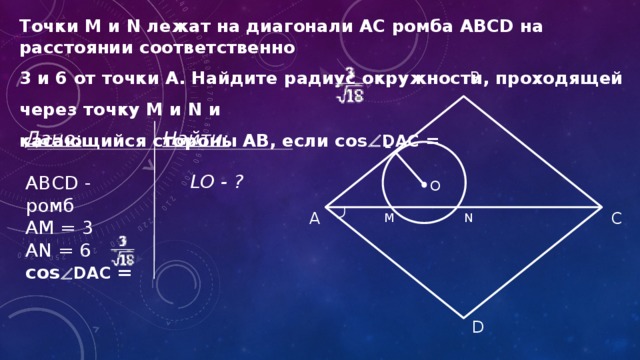
Точки M и N лежат на диагонали АС ромба ABCD на расстоянии соответственно

3 и 6 от точки А. Найдите радиус окружности, проходящей через точку M и N и

касающийся стороны AB, если cos  DAC =

B

Найти:

Дано:

ABCD - ромб АM = 3

AN = 6

cos  DAC =

L

LO - ?

О

C

А

M

N

D

B

Решение:

1. Так как ABCD – ромб, то  ABC =  ADC (по 3ем сторонам).Из равенства треугольников следует равенство соответствующих элементов. Из этого следует что cos  DAC =cos  BAC =

L

О

2. По теореме о касательной и секущей найдем AL.

AL 2 = AM*AN

AL =  18

C

А

M

N

3. Рассмотрим  ALM. По теореме косинусов найдем LM.

LM 2 = AL 2 + AM 2 - 2AM*AL*cos  LAM

LM=3

D

4. Заметим, что AM=LM. Следовательно,  AML-равнобедренный. По свойству

равнобедренного треугольника  ALM =  LAM

B

Решение:

1. Так как ABCD – ромб, то  ABC =  ADC (по 3ем сторонам).Из равенства треугольников следует равенство соответствующих элементов. Из этого следует что cos  DAC =cos  BAC =

L

E

О

2. По теореме о касательной и секущей найдем AL.

AL 2 = AM*AN

AL =  18

А

C

M

N

3. Рассмотрим  ALM. По теореме косинусов найдем LM.

LM 2 = AL 2 + AM 2 - 2AM*AL*cos  LAM

LM=3

D

4. Заметим, что AM=LM. Следовательно,  AML-равнобедренный. По свойству

равнобедренного треугольника  ALM =  LAM

1  

5. По свойству углов, связанных с окружностью :  ALM = 2 LM . Так как  LOM – центральный угол.  LOM =LM .

6. Рассмотрим  LOM, где OL = OM = R. Следовательно, этот треугольник равнобедренный. Проведем к стороне LM высоту.

7. По свойствам равнобедренного треугольника высота является и биссектрисой и медианой. Отсюда следует:

1 1 

 LOE = 2  LOM = 2 LM=  ALM

cos  LOE = cos  ALM = и LE = LM:2 =1.5

B

Решение:

8. По тригонометрической формуле найдем sin  LOE

sin  LOE =  1-cos 2  LOE

2

sin  LOE =  2

По определению: LE

sin  LOE = LO

2 3

 2 2LO

LO = 3  2

L

E

О

C

А

M

N

D

R = 3  2

Ответ: