
ГАПОУ КО «Калужский колледж экономики и технологий»
Многогранники и тела вращения
Урок обобщения, систематизации, контроля и коррекции ЗУН
Подготовила: преподаватель Лавриеня Е.А.
Калуга, 2018

Скажи мне – и я забуду,
Покажи мне – и я запомню,
Дай мне действовать самому –
И я научусь.
Китайская мудрость.

Цель занятия
Обобщение, систематизация, контроль и коррекция знаний и умений по теме:
«Многогранники и тела вращения»

После изучения темы студент должен
Знать:
- Основные понятия темы «Многогранники»: определение призмы, параллелепипеда, пирамиды и усеченной пирамиды;
- Основные элементы многогранников: боковая поверхность, основание, апофема, высота;
- Основные понятия темы «Тела вращения»: определение цилиндра, конуса, усеченного конуса, шара и сферы;
- Основные элементы тел вращения: боковая поверхность, основание, образующая, высота, радиус основания;
- Виды возможных сечений многогранников и тел вращения;
- Формулы площадей и объемов многогранников и тел вращения.
Уметь:
- Изображать на чертеже многогранники и тела вращения;
- Строить сечения многогранников и тел вращения;
- Находить все элементы многогранников и тел вращения;
- Вычислять площади многогранников и тел вращения: полной поверхности, боковой, основания;
- Вычислять объемы многогранников и тел вращения.

План урока:
- Вступительная речь учителя
- Разминка
- Теоретический этап
- Групповое задание
- Индивидуальное задание
- Кроссворд
- Подведение итогов
- Постановка Д/З
Этап № 1
«Разминка»

Дайте определение многогранника
Многогранник - это тело, ограниченное несколькими многоугольниками

Дайте определение призмы
Призма — многогранник, две грани которого равные параллельные многоугольники (основания призмы), а все остальные – параллелограммы (боковая поверхность)

Дайте определение параллелепипеда
Параллелепипед – это призма, в основании которой лежит параллелограмм

Дайте определение пирамиды
Пирамида – это многогранник, одна из граней которого - многоугольник (основание пирамиды), а все другие грани – треугольники (боковая поверхность) с одной общей вершиной (вершина пирамиды)
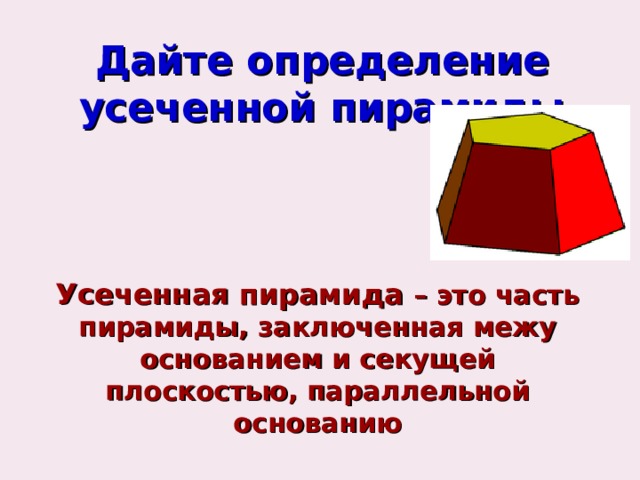
Дайте определение усеченной пирамиды
Усеченная пирамида – это часть пирамиды, заключенная межу основанием и секущей плоскостью, параллельной основанию
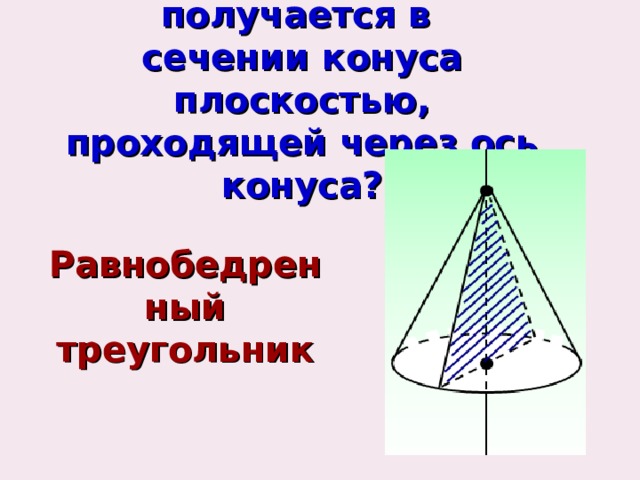
Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса?
Равнобедренный треугольник
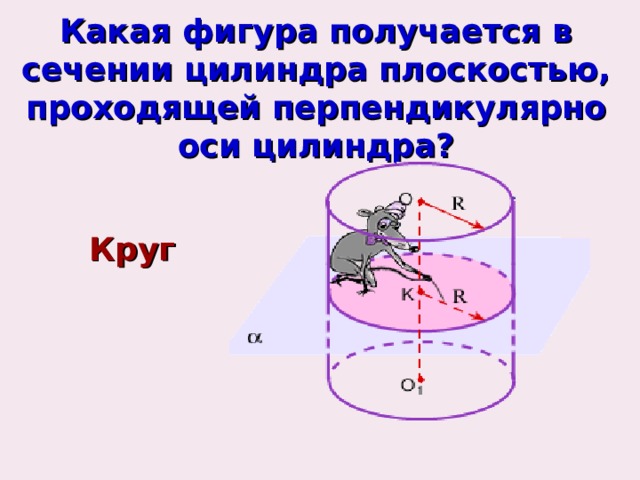
Какая фигура получается в сечении цилиндра плоскостью, проходящей перпендикулярно оси цилиндра?
Круг
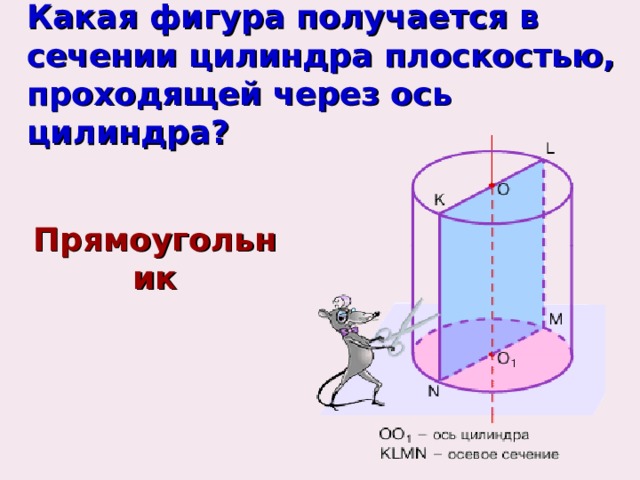
Какая фигура получается в сечении цилиндра плоскостью, проходящей через ось цилиндра?
Прямоугольник

Какая фигура получается в сечении конуса плоскостью, проходящей перпендикулярно оси конуса?
Круг
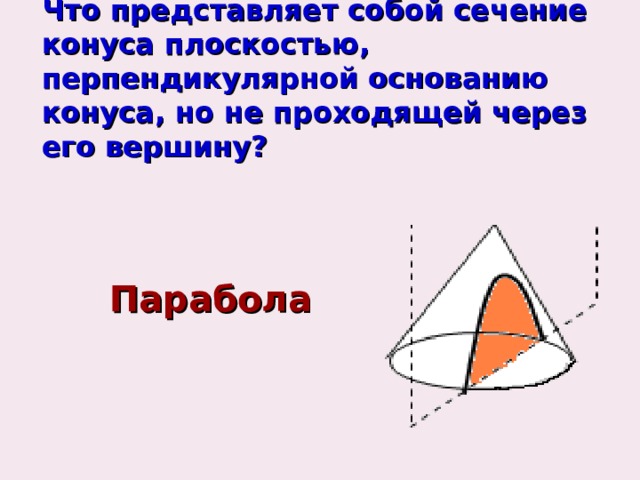
Что представляет собой сечение конуса плоскостью, перпендикулярной основанию конуса, но не проходящей через его вершину?
Парабола

Цилиндр можно получить путем вращения …
… прямоугольника, вокруг одной из его сторон
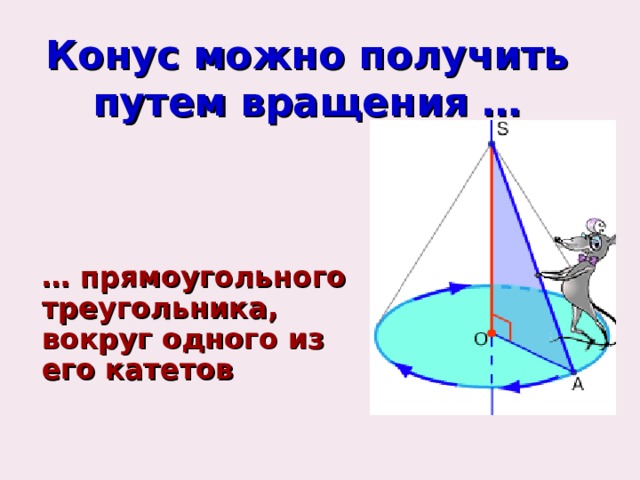
Конус можно получить путем вращения …
… прямоугольного треугольника, вокруг одного из его катетов
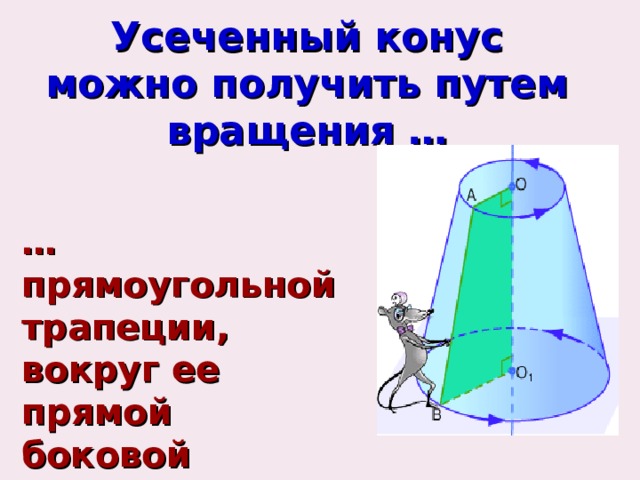
Усеченный конус можно получить путем вращения …
… прямоугольной трапеции, вокруг ее прямой боковой стороны

Шар можно получить путем вращения …
… полукруга вокруг его диаметра
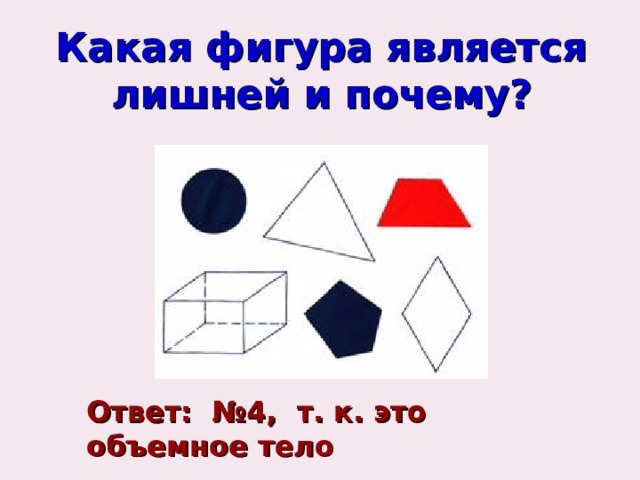
Какая фигура является лишней и почему?
Ответ: №4, т. к. это объемное тело
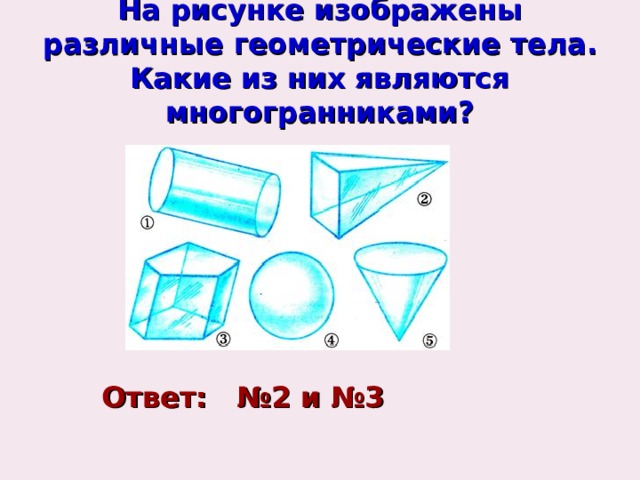
На рисунке изображены различные геометрические тела. Какие из них являются многогранниками?
Ответ: №2 и №3

Этап № 2
«Теоретическое задание»

Многогранники
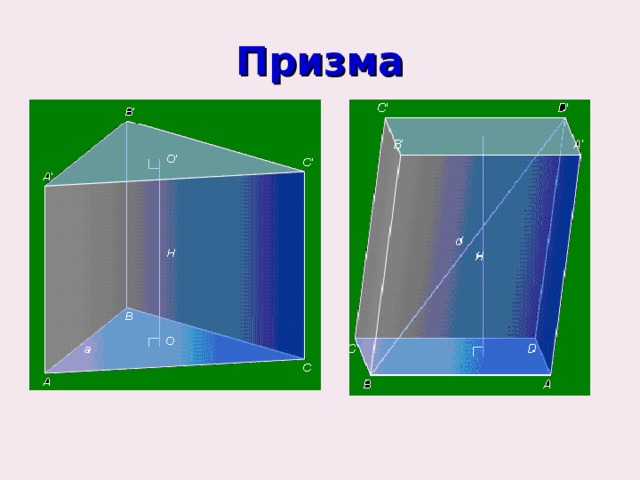
Призма
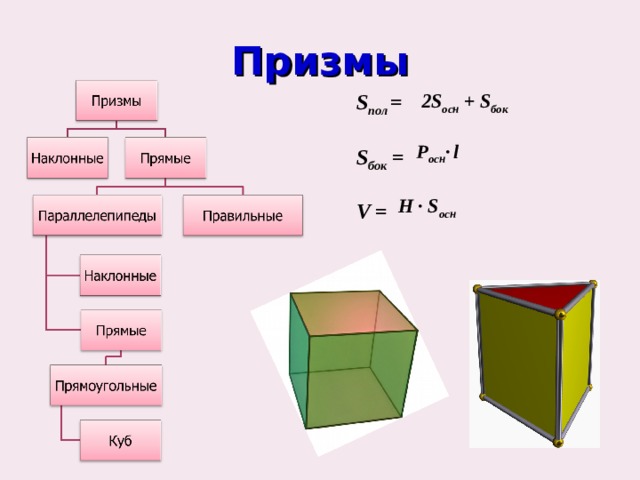
Призмы
S пол =
S бок =
V =
2 S осн + S бок
Р осн ∙ l
H ∙ S осн
Пирамиды
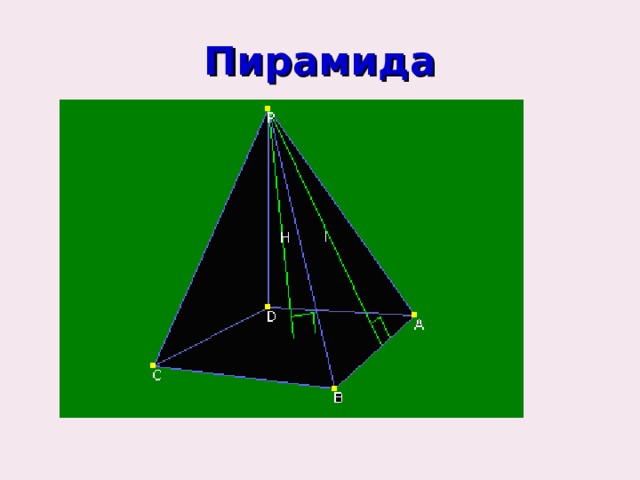
Пирамида
S пол = S осн + S бок
S бок = Р осн ∙ l
V = H ∙ S осн
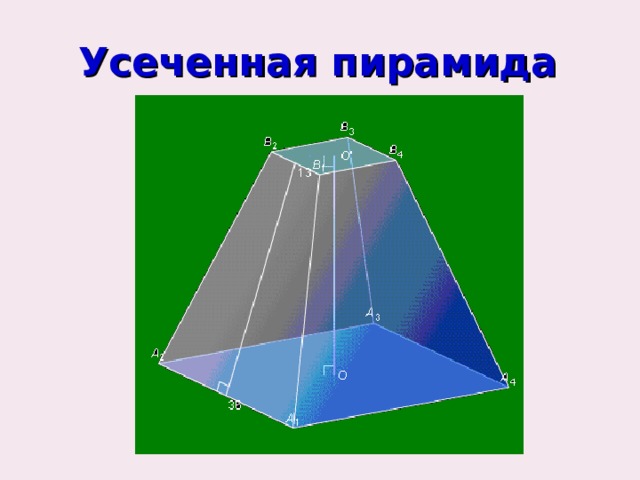
Усеченная пирамида

Площадь полной поверхности и объем усеченной пирамиды
S пол = S осн1 + S бок + S осн2
S бок = ∙ l ∙ (Р осн1 + Р осн2 )
V = H ∙ ( S осн1 + S осн2 + )

Тела вращения
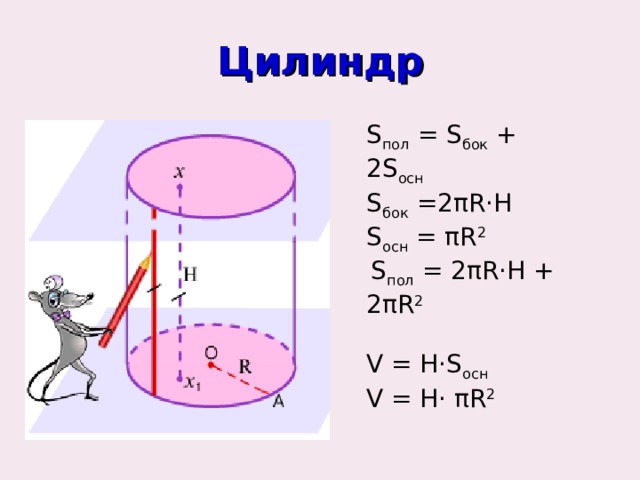
Цилиндр
S пол = S бок + 2S осн
S бок = 2 π R·H
S осн = π R 2
S пол = 2 π R·H + 2 π R 2
V = H·S осн
V = H· π R 2
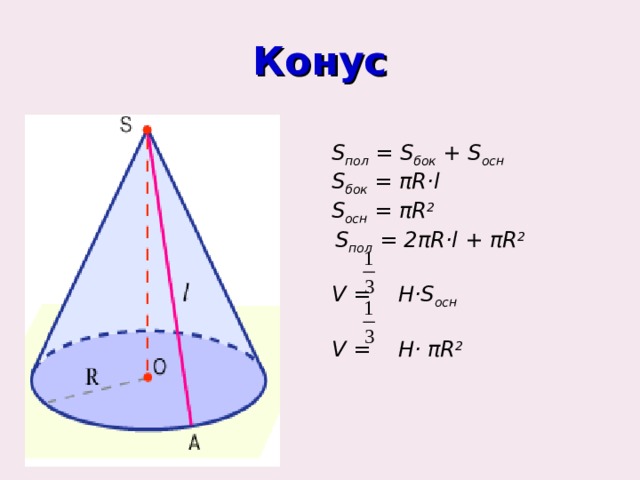
Конус
S пол = S бок + S осн
S бок = π R·l
S осн = π R 2
S пол = 2 π R·l + π R 2
V = H·S осн
V = H· π R 2
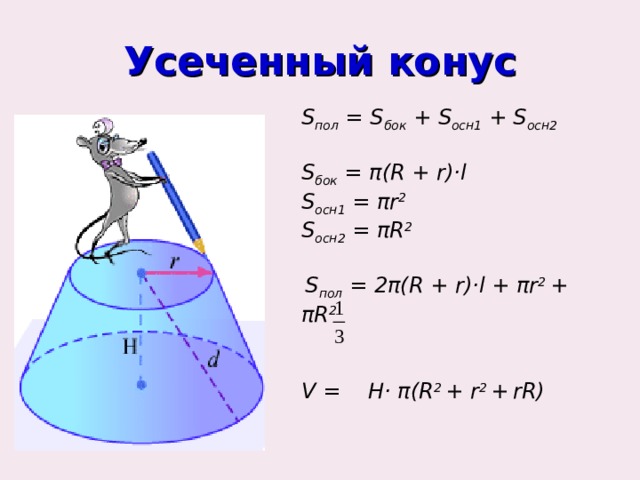
Усеченный конус
S пол = S бок + S осн 1 + S осн 2
S бок = π ( R + r)·l
S осн 1 = π r 2
S осн 2 = π R 2
S пол = 2 π ( R + r)·l + π r 2 + π R 2
V = H· π ( R 2 + r 2 + r R)
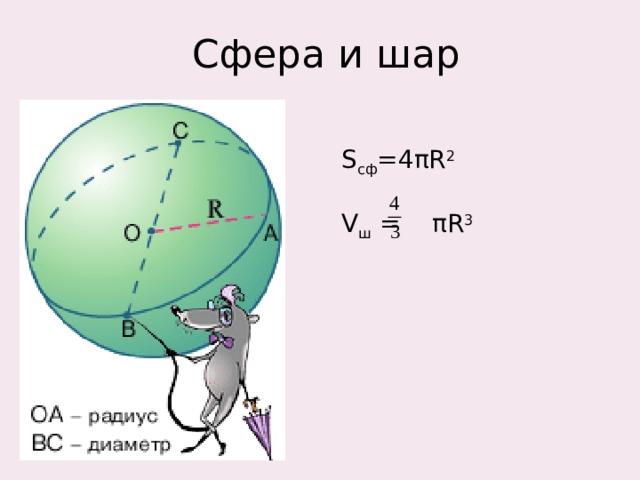
Сфера и шар
S сф =4 π R 2
V ш = π R 3


Этап № 3
«Групповое задание»
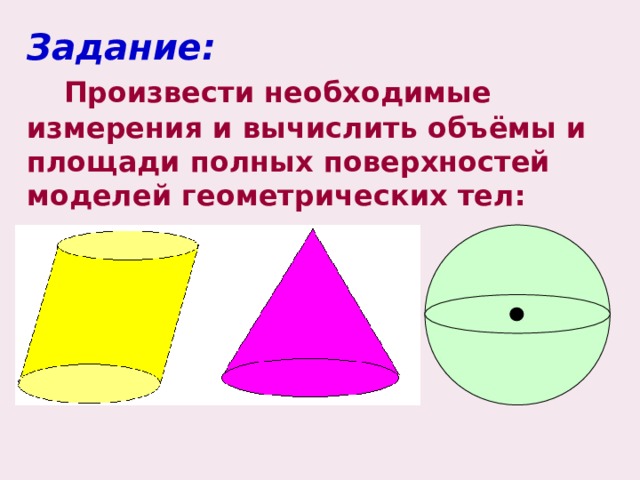
Задание: Произвести необходимые измерения и вычислить объёмы и площади полных поверхностей моделей геометрических тел:

Этап № 4
«Индивидуальное письменное задание»
39

Критерии оценки:
- Правильное оформление условия задачи (дано, требуется найти, рисунок) – 1-2 балла;
- Ход решения и обоснование к нему – 2-3 балла;
- Верный получившийся ответ – 1-2 балла.
Этап № 5
«Кроссворд»
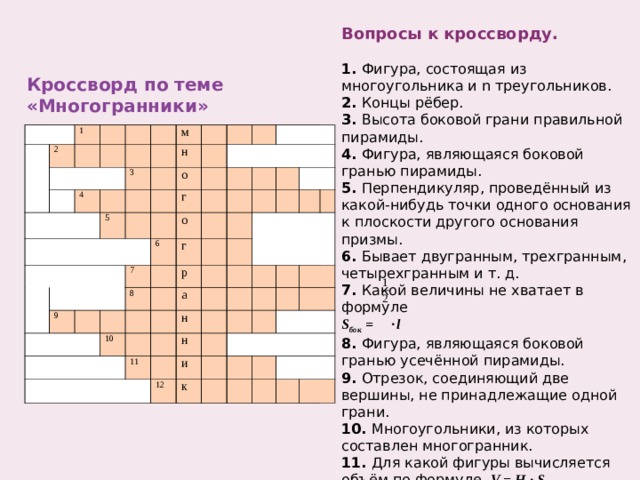
Вопросы к кроссворду.
1. Фигура, состоящая из многоугольника и n треугольников.
2. Концы рёбер.
3. Высота боковой грани правильной пирамиды.
4. Фигура, являющаяся боковой гранью пирамиды.
5. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания призмы.
6. Бывает двугранным, трехгранным, четырехгранным и т. д.
7. Какой величины не хватает в формуле
S бок = ∙ l
8. Фигура, являющаяся боковой гранью усечённой пирамиды.
9. Отрезок, соединяющий две вершины, не принадлежащие одной грани.
10. Многоугольники, из которых составлен многогранник.
11. Для какой фигуры вычисляется объём по формуле V = H ∙ S осн
12. Правильный многогранник, состоящий из 8 равносторонних треугольников.
Кроссворд по теме «Многогранники»
2
1
1
2
4
4
м
3
3
м
5
н
5
н
о
о
г
9
6
о
г
7
9
г
7
8
6
о
8
г
10
р
10
а
р
11
н
а
н
н
11
н
12
и
12
к
и
к
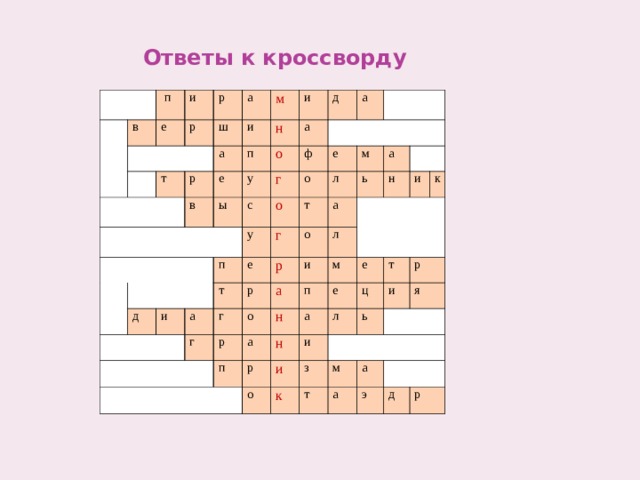
Ответы к кроссворду
в
п
и
е
р
р
а
ш
т
м
и
а
р
и
н
е
п
в
у
о
д
а
ы
д
ф
а
г
с
и
у
о
п
о
е
т
т
а
л
г
м
е
г
г
р
р
а
ь
о
а
и
р
о
л
а
н
н
м
а
п
п
и
е
р
е
а
н
к
л
и
ц
и
о
т
к
ь
з
р
и
т
м
я
а
а
э
д
р

Домашнее задание
- Повторить теорию по теме «Многогранники и тела вращения»
- Решить две задачи
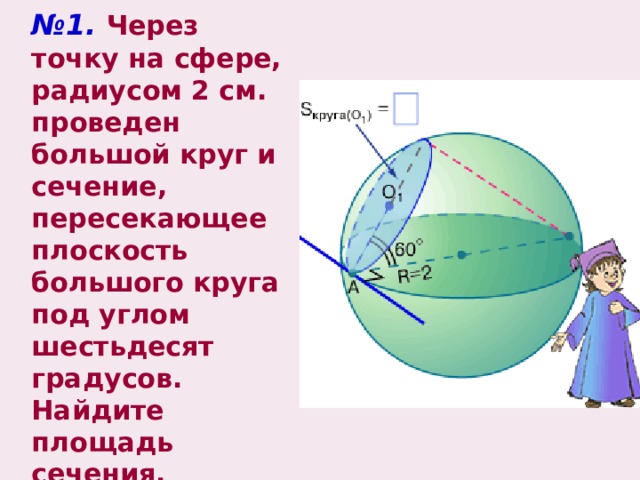
№ 1. Через точку на сфере, радиусом 2 см. проведен большой круг и сечение, пересекающее плоскость большого круга под углом шестьдесят градусов. Найдите площадь сечения.
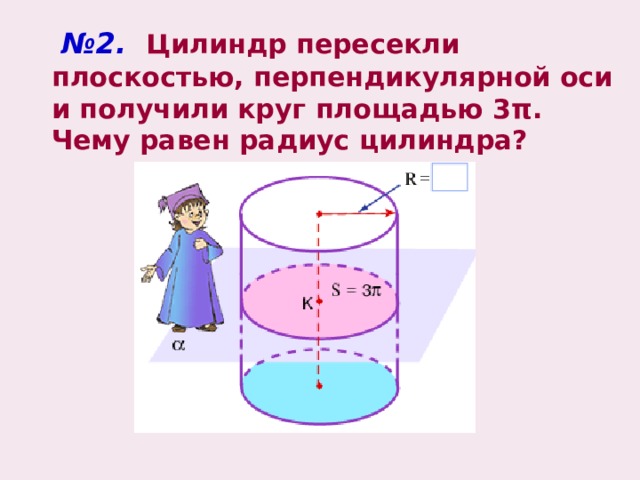
№ 2. Цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3 π . Чему равен радиус цилиндра?

Спасибо за внимание





