Математические диктанты для 7 класса

Для чего нужны диктанты

Одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Это пригодится учащимся в жизни – умение слушать лекцию, слушать собеседника, слушать и «слышать». Кроме того, важно формировать у обучающихся грамотную математическую речь. Использование математических диктантов помогает в решении вышеуказанных задач.

Математические диктанты необходимо использовать систематически. Если приучать детей к диктантам с 5 класса, то постепенно они привыкают к такой форме работы. При работе с математическими диктантами учащиеся меньше переспрашивают, понимают задания после 1–2 прочтений вопроса, выполняют правильно большую часть диктанта, а также учатся самостоятельно правильно осмысливать учебные задания.

Математические диктанты для 7 класса

Выражения

Вариант 1

1. Запишите пример числового выражения.

2. Найдите значение выражения: 9,6 – 3 ∙ 1,2.

3. Запишите в виде выражения: сумма числа 7 и частного чисел 30 и 5.

4. Запишите в виде выражения: квадрат числа х.

5. Найдите значение выражения , если .

6. Напишите формулу чётного числа.

7. При каких значениях переменной не имеет смысла выражение: ?

8. Напишите пример строгого неравенства.

9. Запишите в виде неравенства: у – неотрицательное число.

10. Запишите в виде двойного неравенства: 0,47 больше 0,4 и меньше 0,5.

11. Как читается знак “≥” ?

12. Сравните х + 3 и 3х при х = 2.

Вариант 2

1. Запишите пример выражения с переменными.

2. Найдите значение выражения: 2 ∙ 1,7 + 3,6.

3. Запишите в виде выражения: разность произведения 2 и 4 и числа 8.

4. Запишите в виде выражения: куб числа у.

5. Найдите значение выражения , если .

6. При каких значениях переменной не имеет смысла выражение: ?

7. Напишите формулу нечётного числа.

8. Запишите в виде неравенства: х – отрицательное число.

9. Напишите пример нестрогого неравенства.

10. Запишите в виде двойного неравенства: 1,6 больше 0,9 и меньше 2,1.

11. Как читается знак “≤” ?

12. Сравните 5у и у – 2 при у = 3.

Ответы

Вариант 1	Вариант 2
1. 35 + 4	1. х – 10
2. 6	2. 7
3. 7 + 30 : 5	3. 2  4 – 8
4. х2	4. у3
5. – 18	5. 19
6. 2 n, где n – натуральное число	6. при
7. При	7. 2n + 1, где n – натуральное число
8. 10 4	8. х
9. у ≥ 0	9. х ≤ 4
10. 0, 4	10. 0, 9
11. Больше или равно	11. Меньше или равно
12. 5	12. 15 1

Уравнения

Вариант 1

1. Как найти неизвестный множитель?

2. Как найти неизвестное уменьшаемое?

3. Как найти неизвестный делитель?

4. Дайте определение корня уравнения.

5. Какое уравнение называется линейным?

6. В каком случае уравнение имеет бесконечно много корней?

7. Является ли 5 корнем уравнения 2х + 3 = 18?

8. В каком случае уравнение не имеет корней?

9. Запишите первое свойство уравнений.

Вариант 2

1. Как найти неизвестное слагаемое?

2. Как найти неизвестное делимое?

3. Как найти неизвестное вычитаемое?

4. Что значит “решить уравнение”?

5. Какие уравнения называются равносильными?

6. В каком случае уравнение имеет единственный корень?

7. Является ли 2 корнем уравнения 11 – 3у = 6?

8. Приведите пример линейного уравнения с одной переменной.

9. Запишите второе свойство уравнений.

Ответы

Вариант 1	Вариант 2
1. Произведение разделить на известный множитель.	1. От суммы отнять известное слагаемое.
2. К разности прибавить вычитаемое.	2. Делитель умножить на частное.
3. Делимое разделить на частное.	3. От уменьшаемого отнять разность.
4. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.	4. Решить уравнение – значит найти все его корни или доказать, что корней нет.
5. Уравнение вида , где х – переменная, и – некоторые числа.	5. Уравнения, имеющие одни и те же корни.
6. При = 0 и = 0	6. При
7. Да.	7. Нет.
8. При = 0 и	8. 3х = 5
9. Если в уравнении перенести слагаемое из одной части уравнения в другую, изменив его знак, то получится уравнение, равносильное данному	9. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному

Определение функции

Вариант 1

1. Дайте определение линейной функции.

2. Как расположен график функции у = k x, если k

3. Функция задана формулой у = 3х – 7. Найдите значение функции, если аргумент равен –2.

4. Что является графиком прямой пропорциональности?

5. Дана функция у = 2 – 7 х. Чему равно k?

6. Дана функция у = 3 + 4х. Чему равно b?

7. В каком случае графики двух линейных функций пересекаются?

Вариант 2

1. Формулой какого вида задаётся прямая пропорциональность?

2. Что является графиком линейной функции?

3. Функция задана формулой у = 5 – 2х. Найдите значение функции, если аргумент равен 4.

4. Как расположен график функции у = k x, если k 0 ?

5. Дана функция у = – 3 – 10х. Чему равно b?

6. Дана функция у = 8 – х. Чему равно k?

7. В каком случае графики двух линейных функций параллельны?

Ответы

Вариант 1	Вариант 2
1. у = k х + b, где х – аргумент, k и b – числа	1. у = k х, k 0, где k – аргумент
2. Проходит через начало координат, во II и IV координатных четвертях	2. Прямая
3. у = – 13	3. у = – 3
4. Прямая, проходящая через начало координат	4. Проходит через начало координат, во I и III координатных четвертях
5. k = – 7	5. b = – 3
6. b = 3	6. k = – 1
7. Коэффициенты не равны, k1 k2	7. Коэффициенты равны k1 = k2

Степень с натуральным показателем

Вариант 1

1. Как называется выражение ?

2. Как называется в записи ?

3. Представьте в виде произведения: х⁴.

4. Чему равно ?

5. Каким числом является степень положительного числа?

6. Каким числом является степень отрицательного числа с нечётным показателем?

7. Запишите с помощью букв правило умножения степеней с одинаковым основанием.

8. Запишите с помощью букв правило возведения степени в степень.

9. Запишите в виде степени: у¹⁰: у⁵.

10. Запишите в виде произведения: (2х)⁴.

Вариант 2

1. Как называется в записи ?

2. Запишите короче: .

3. Как называется действие нахождения значения степени?

4. Какой показатель у ?

5. Каким числом является степень отрицательного числа с чётным показателем?

6. Сравните с нулём квадрат произвольного числа.

7. Запишите с помощью букв правило деления степеней с одинаковым основанием.

8. Запишите с помощью букв правило возведения в степень произведения двух множителей.

9. Запишите в виде степени: х⁵х⁴х.

10. Запишите в виде степени: (х²)³.

Ответы

Вариант 1	Вариант 2
1. Степень числа	1. Основание степени
2. Показатель степени	2.
3. х4 = х х х х	3. Возведение в степень
4. = 1	4.
5. Положительное число	5. Положительное число
6. Отрицательное число	6. 0
7.	7. , где
8.	8.
9. х5	9. х10
10. 16 х4	10. х6

Одночлены

Вариант 1

1. Приведите пример одночлена стандартного вида второй степени.

2. Запишите определение степени одночлена.

3. Запишите данный одночлен 6 х³х в стандартном виде.

4. Запишите коэффициент одночлена – 4х.

5. Какова степень одночлена 2 ?

6. Представьте одночлен 0,09 у⁴ в виде квадрата.

7. Какой одночлен надо возвести в куб, чтобы получить одночлен

125х⁶у⁹?

Вариант 2

1. Приведите пример одночлена стандартного вида первой степени.

2. Какую степень имеет одночлен, не содержащий переменных?

3. Запишите данный одночлен в стандартном виде 2у 3х.

4. Какова степень одночлена 5 ?

5. Запишите коэффициент одночлена ху.

6. Представьте одночлен 27х⁶ в виде куба.

7. Какой одночлен надо возвести в квадрат, чтобы получить одночлен 10000 ?

Ответы

Вариант 1	Вариант 2
1. 10ху	1. 4у
2. Сумма показателей степеней всех входящих в него переменных	2. Если одночлен не содержит переменных, то его степень считают равной нулю
3. 6х4	3. 6ху
4. – 4	4. 3
5. 5	5. 1
6. (0,3 у2)2	6. (3х2)3
7. 5х2у3	7. 100

Многочлены

Вариант 1

1. Дайте определение многочлена.

2. Приведите пример многочлена третьей степени.

3. Приведите пример двучлена.

4. Запишите многочлен в стандартном виде: 5х  3х² – 2у³ 4у.

5. Какую степень имеет многочлен ?

6. Расположите по убывающим степеням переменной многочлен:

34 – с⁶ + 5с² – с⁴.

7. Найдите сумму многочленов: – – и – .

8. В многочлене 5х² – х + 4 заключите в скобки два последних члена, поставив перед скобками знак “плюс”.

9. Умножьте многочлены: х + 2 и у – 3.

10. Какое преобразование называют разложением многочлена на множители?

Вариант 2

1. Что называется степенью многочлена?

2. Приведите пример многочлена второй степени.

3. Приведите пример трёхчлена.

4. Запишите многочлен в стандартном виде: .

5. Какую степень имеет многочлен ?

6. Расположите по возрастающим степеням переменной многочлен:

2у + у³ – у² + 1.

7. Найдите разность многочленов: – и + .

8. В многочлене 2у³ + у – 3 заключите в скобки два последних члена, поставив перед скобками знак “минус”.

9. Умножьте многочлены: n – 5 и p – 2.

10. Сформулируйте правило умножения одночлена на многочлен.

Ответы

Вариант 1	Вариант 2
1. Многочленом называется сумма одночленов	1. Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов
2. 41х3 – 5	2. 17ху + 5у
3. 3у + 4	3. 3х2 + х – 5
4. 15 х3 – 8 у4	4.
5. 4	5. 5
6. –с6 – с4 + 5с2 + 34	6. 1 + 2у – у2 + у3
7. – 2	7. – 2
8. 5х2 + (–х + 4)	8. 2у3 – (–у + 3)
9. ху – 3х + 2у – 6	9. n p – 2 n – 5 p + 10
10. Представление многочлена в виде произведения нескольких многочленов	10. Нужно умножить одночлен на каждый член многочлена, и полученные произведения сложить

Формулы сокращённого умножения

Вариант 1

1. Закончите формулу

2. Закончите формулу .

3. Закончите формулу .

4. Представьте в виде многочлена: (2 – х)².

5. Представьте трёхчлен в виде квадрата двучлена:

у² + 12у + 36.

6. Выполните умножение: .

7. Разложите на множители: 169 – 4х².

8. Запишите выражение в виде произведения: .

Вариант 2

1. Закончите формулу .

2. Закончите формулу .

3. Закончите формулу .

4. Представьте в виде многочлена: (у + 3)².

5. Представьте трёхчлен в виде квадрата двучлена: 64 – 16х + х².

6. Выполните умножение: .

7. Разложите на множители: 9у² – 121.

8. Запишите выражение в виде произведения: .

Ответы

Вариант 1	Вариант 2
1. … = .	1. … =
2. … =	2. … = .
3. … =	3. … =
4. 4 – 4х + х2	4. у2 + 6у + 9
5. (у + 6)2	5. (8 – х)2
6.	6.
7. (13 – 2х) (13 + 2х)	7. (3у –11) (3у + 11)
8.	8. (х3 –5) (х6 + 5х + 25)

Система линейных уравнений

Вариант 1

1. Дайте определение линейного уравнения с двумя переменными.

2. Является ли данное уравнение линейным уравнением с двумя переменными: 4х + у² = 3?

3. Запишите какое-либо решение уравнения: х – у = 8.

4. Является ли пара чисел х = – 2 и у = 1 решением уравнения:

2х + у = – 3?

5. Выразите у через х из уравнения 6х – у = 12.

6. Что называется решением системы уравнений с двумя переменными?

7. Составьте какую-либо систему линейных уравнений с переменными х и у.

8. Каким способом удобнее решать систему?

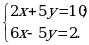
Вариант 2

1. Что называется решением уравнения с двумя переменными?

2. Приведите пример линейного уравнения с двумя переменными.

3. Запишите какое-либо решение уравнения: х + у = 20.

4. Является ли пара чисел х = 7 и у = – 1 решением уравнения:

х – 3у = 4?

5. Выразите х через у из уравнения х – 3у = 1.

6. Что является графиком линейного уравнения с двумя переменными?

7. Сколько решений может иметь система двух линейных уравнений с двумя переменными?

8. Каким способом удобнее решать систему?

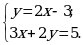
Ответы

Вариант 1	Вариант 2
1. Линейным уравнением с двумя переменными называется уравнение вида , где х и у – переменные, и – некоторые числа	1. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство
2. Нет	2. 5х + 3у = 7
3. (10; 2)	3. (13; 7)
4. Да	4. Нет
5. у = 6х – 12	5. х = 1 + 3у
6. Решением систем уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство	6. Множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения
7. 9х – 4у = 2	7. Одно или ни одного решения
8. Способом сложения	8. Способом подстановки

Используемые материалы.

Математика 7-9 классы. Методические материалы к урокам. Современные требования. Педагогические мастерские./ Издательство «Учитель»