Изображение фигур в пространстве

Дисциплина ОУДП. Математика: алгебра, начала математического анализа, геометрия

Группы 1 курса ППКРС топ-50

ПЛАН ЗАНЯТИЯ № 71

Тема программы №4: Прямые и плоскости в пространстве

Тема занятия 17: Изображение пространственных фигур

Цель занятия: изучить способы построения изображений плоских и пространственных фигур на плоскости.

Задачи занятия:

1. закрепление понятия «параллельное проецирование» и его свойств, формирование навыков построения изображений плоских и пространственных фигур на плоскости с помощью аксонометрической проекции

2. развитие пространственного воображения, познавательного интереса, внимания

3. развитие навыков коллективной работы, организованности, создание атмосферы доброжелательности на уроке.

Тип занятия: объяснение нового материала

Материально-техническое обеспечение занятия:

Дидактическое обеспечение: плакаты для дидактической игры

Инструменты и оборудование: линейка, угольник, модели геометрических тел

Информационное обеспечение занятия:

Литература: [2] Геометрия. 10—11 классы: базовый и углубленный уровни / Л. С. Атанасян, В.Ф. Бутузов и др. - М.: Просвещение, 2014.

[7] Геометрия. 10 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики / Е.В. Потоскуев, Л.И. Звавич. – М.: Дрофа, 2015.

Интернет-ресурсы: https://youclever.org/book/izobrazhenie-prostranstvennyh-figur-1

Формирование компетенций в соответствии с ФГОС:

ОК 2. Организовывать собственную деятельность, исходя из цели и способов ее достижения, определенных руководителем.

ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.

ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.

ОК 6. Работать в команде, эффективно общаться с коллегами, руководством, клиентами.

Ход занятия

1. Организационный момент (1 мин):

приветствие, проверка явки и готовности к занятию

2. Актуализация знаний (повторение изученного материала) (9 мин)

Дидактическая игра «Верно – неверно». Этап сопровождается показом плакатов.

Преподаватель: Чтобы работа на уроке была плодотворной, давайте вспомним некоторые факты, характеризующие параллельное проектирование и его свойства. Ваша задача определить верность следующих высказываний. В случае противоречия, привести теоретическое обоснование. Итак, начинаем.

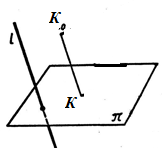
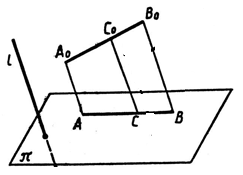
1. Параллельное проектирование состоит в следующем: берём произвольную прямую «l», пересекающую плоскость чертежа «π», проводим через произвольную точку К₀ фигуры прямую, параллельную прямой «l». Верно, ли что точка К пересечения этой прямой с плоскостью чертежа будет изображением точки К₀? (см. рис. 1 на доске)

Ответ: Верно.

2. Верно ли, что прямая, проведённая через точку К₀ параллельно прямой «l», может не пересечь плоскость «π»? (см. рис. 1 на доске)

Ответ: Неверно. По лемме о пересечении плоскости двумя параллельными прямыми, если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

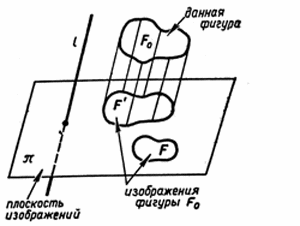
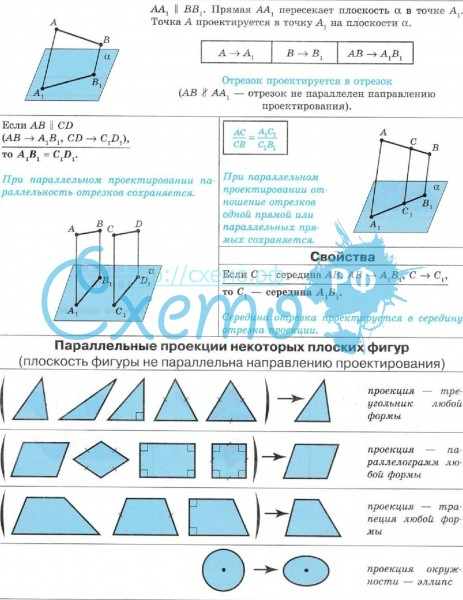
3. Верно ли, чтобы получить изображение пространственной фигуры на плоскости, необходимо построить изображение каждой точки фигуры с помощью параллельного проектирования? (см. рис. 2 на доске)

Ответ: Верно.

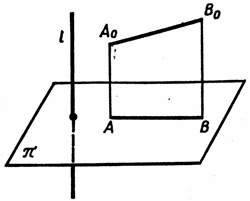
4. Верно ли, что проекцией отрезка на плоскость является прямая? (см. рис. 3 на доске)

Ответ: Неверно. Проекция отрезка есть отрезок.

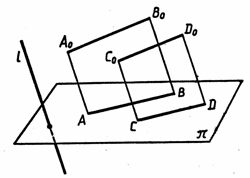
5. Верно ли, что проекцией параллельных отрезков являются параллельные отрезки? (см. рис. 4 на доске)

Ответ: Верно.

6. Верно ли, что середина отрезка проецируется в произвольную точку отрезка проекции? (см. рис. 5 на доске)

Ответ: Неверно. Середина отрезка проецируется в середину отрезка, так как при параллельном проектировании отношение отрезков сохраняется.

Рис. 1	Рис. 2	Рис. 3
Рис. 4	Рис. 5

Преподаватель: Вы заметили, что дать точный ответ нам помогли чертежи.

3. Сообщение темы, цели занятия, критериев оценки (2 мин)

Преподаватель: Продолжим наше занятие с разгадывания ребуса.

Ответ: Изображение фигур

Записываем тему занятия: Изображение пространственных фигур.

При изучении стереометрии и решении задач мы будем пользоваться чертежами: они помогут нам представить, проиллюстрировать содержание того или иного факта, суть понятия, понять то, о чем идет речь в задаче или теореме.

Однако при строгом подходе к изучению геометрии рисунок не имеет доказательной силы, даже если он выполнен безупречно. И тем не менее, наглядно и хорошо выполненный рисунок (чертеж) к задаче – это надежный помощник при ее решении.

Цель занятия: изучить способы построения изображений пространственных фигур на плоскости, которые выполняются на основе математических законов.

Критерии оценивания:

На занятии получать отметки те обучающиеся, которые будут активно работать на занятии. На выбор будут проверены рабочие тетради.

4. Объяснение нового материала (28 мин)

Преподаватель: Изучать способы построения изображений пространственных фигур на плоскости будем, работая в группах.

Преподаватель проводит инструктаж: Каждая группа в течение 6 минут будет изучать способ построения некоторого геометрического тела. Затем один или двое обучающиеся из группы объяснят изученный их группой материал (20 минут, каждая группа по 4 минуты).

Обучающиеся все необходимые записи делают в своих рабочих тетрадях.

Группа №1: Изображение плоских фигур на плоскости.

Отметим, что плоскость фигуры не параллельна направлению проектирования.

	Проекция – треугольник любой формы
	Проекция – параллелограмм любой формы
	Проекция – трапеция любой формы
	Проекция окружности – эллипс (овал)

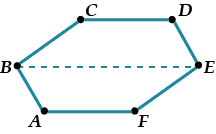
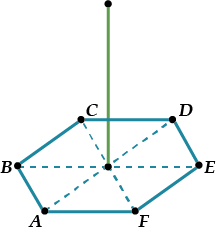
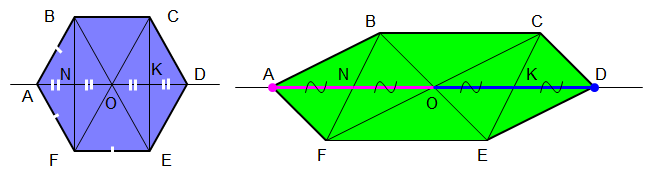
Группа №2: Изображение правильного шестиугольника.

Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника ΔFAB и ΔCDE.

Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE.

Осталось найти местоположение двух оставшихся вершин – точек A и D.

Вспомнив свойства правильного шестиугольника, заметим, что:

1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE;

2) OK=KD и ON=NA.

Значит:

1. находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K;

2. откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.

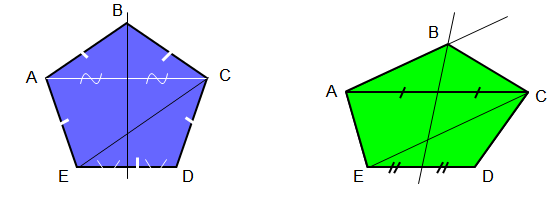
Группа №3: Изображение правильного пятиугольника.

Разобьем правильный пятиугольник на две части – равнобокую трапецию АСDЕ и равнобедренный треугольник ΔАВС.

Построим вначале изображение равнобокой трапеции АСDЕ – произвольная трапеция АСDЕ.

Осталось найти местоположение оставшейся вершины – точки В.

Вспомнив свойства правильного пятиугольника, заметим, что:

1) вершина В лежит на прямой, проходящей, например, через вершину А и параллельной диагонали ЕC;

2) вершина В лежит на серединном перпендикуляре, проведенном через противоположную сторону пятиугольника ЕD.

Значит:

1. находим на изображении середины отрезков ЕD и АС и проводим через неё прямую;

2. проводим прямую через вершину А, параллельно отрезку ЕС, до пересечения с серединным перпендикуляром – в итоге получаем оставшуюся вершину правильного пятиугольника В.

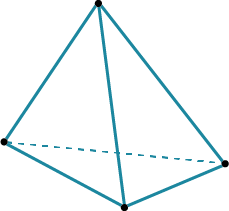
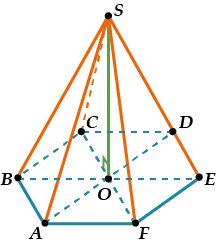
Группа №4: Изображение пирамиды.

Треугольная пирамида

Для изображения треугольной пирамиды, нужно сначала нарисовать «косой» четырехугольник.

А потом добавить еще два ребра, с учетом видимых и невидимых ребер.

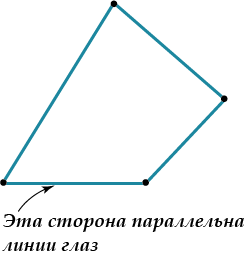
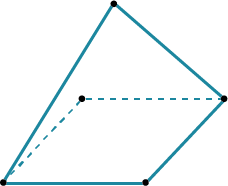
С четырехугольной пирамидой сложнее, но тоже разумно сперва прорисовать контур, а потом добавлять ребра.

В исходном четырех-угольнике одна из сторон должна быть параллельна взгляду.

Потом проводим отрезки, параллельные двум сторонам. Получаем параллелограмм.

Осталось только соединить оставшиеся вершины.

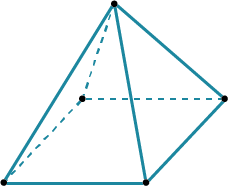
И осталось самое сложное – шестиугольная пирамида. Чаще всего нужна правильная.

Здесь уже сперва основание!

Потом из центра основания провести перпендикуляр, чтобы легче найти вершину.

И потом уже соединить вершину с вершинами основания.

Преподаватель: И не думайте, что шестиугольная пирамида получится с первого раза – нужно тренироваться!

Группа №5: Изображение параллелепипеда и призмы.

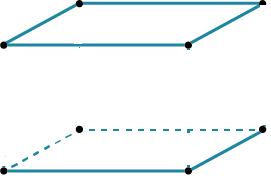
Параллелепипед

Сначала нужно нари-совать основание в виде параллелограмма.

Потом второе основание, равное первому и параллельно ему.

И потом уже соединить вершины верхнего основания с вершинами нижнего основания.

Главное – соблюдать параллельность.

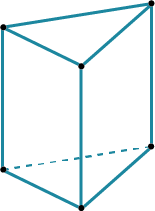
Чаще всего при решении задач используется треугольная призма.

Сначала нужно нари-совать основание в виде треугольника. Лучше угол треугольника смотрел на нас - живее получится.

А затем боковые ребра, равной длины и параллельных друг другу.

И потом верхнее основание, соединив концы ребер.

5. Подведение итогов занятия, оценивание работы (3 мин)

Преподаватель: Такой способ изображения пространственной фигуры на плоскости соответствует зрительному восприятию фигуры, при рассмотрении её издали. Одну и ту же фигуру можно изобразить по разному. Обычно выбирают то изображение, которое создает правильное представление о форме фигуры.

Вопрос для обсуждения:

Пригодились ли свойства параллельного проектирования при построении изображений геометрических тел? Если да, перечислите их.

Преподаватель: Надеюсь, что никто из Вас не станет отрицать того, что «хороший» чертёж всегда поможет нам в решении геометрических задач.

На практическом занятии, которое будет на следующем уроке, мы будем закреплять способы и правила построения пространственных фигур.

6. Рефлексия

Предлагаю обучающимся закончить предложения на выбор:

• сегодня я узнал…

• было интересно…

• было трудно…

7. Домашнее задание

[2] с. 224-225. Прочитать материал в учебнике.

Преподаватель: Кулева О.В.

Приложение 1

2 = О

ˮ

,#ʼ

2 = У

Приложение 2

Дополнительно:

Преподаватель: Обратим внимание на тот факт, что плоское изображение, подчиняясь определенным законам, способно передать впечатление о трехмерном предмете. Однако при этом могут возникать иллюзии. В живописи существует целое направление, которое называется импоссибилизм (impossibility - невозможность) - изображение невозможных фигур, парадоксов.

Современный шведский архитектор Оскар Рутерсвард посвятил невозможным объектам серию своих художественных работ (см. рис. ).