Из опыта работы

ГБОУ СПО

« Семеновский индустриально художественный техникум»

Организация самостоятельной работы
на уроках математики как средство саморазвития студентов

Выполнила преподаватель математики:

Савельичева И.А.

г. Семенов
2014

Содержание:

1. Информация об опыте………………………………........ 3

2. Технология опыта……………………………………...... 7

3. Результативность опыта………………………………… 13

4. Библиографический список…………………………… 15

5. Приложения к опыту……………………………………..16

Раздел I. Информация об опыте

Согласно социально-психологическому паспорту ОУ ГБОУ СПО СИХТ, большинство учащихся живут в семьях, в которых родители имеют среднее и средне-специальное образование. Студенты поступают в ОУиз разных районов нашей области, поэтому состав учащихся неоднороден по своей подготовленности и развитию. Следовательно целью на уроках и внеурочной деятельности ставиться, прежде всего, развитие личности, интеллекта и самостоятельности студента в такой степени, чтобы он, будучи выпускником, был способен не только самостоятельно находить и усваивать готовую информацию, но и креативно мыслить.

Н.А.Половникова называет три уровня развития познавательной самостоятельности учащихся, положив в основу степень владения методами самостоятельной познавательной деятельности.

На первом уровне – копирующая самостоятельность –студент овладевает образцами всех типичных для его возраста форм познавательной деятельности по предмету. В основном, здесь подразумевается овладение алгоритмическими действиями (по аналогии, по заранее представленному плану и т.п.), ведущими всех учащихся при одинаковых исходных данных к определенному, одинаковому результату.

Второй уровень – воспроизводяще-выборочная (репродуцирующая) самостоятельность – характеризуется самостоятельным воспроизведением основных методов, соответствующих ступени обучения студента, способностью к выбору и использованию нужного метода.

Третий уровень познавательной самостоятельности – творческая самостоятельность студентов – состоит прежде всего в уяснении конструктивного подхода к творчеству, в создании новых методов познавательной самостоятельности на основе уже усвоенных.

Началом работы по теме стало проведение диагностики по определению уровня самостоятельности.

копирующая самостоятельность	репродуцирующая самостоятельность	творческая самостоятельность
70%	5%	0%

Психофизиологические особенности учащихся, разные уровни их умственных способностей, закономерно требуют для обеспечения эффективного учебного процесса каждого студента или группы детей неодинаковых условий обучения.

Поэтому встал вопрос, как организовать обучение, чтобы оно осуществлялось на оптимальном уровне трудности и способствовало развитию всех учащихся, в том числе и самых слабых, и самых сильных.

Важность этой проблемы побудила начать работу по изучению теоретических и практических аспектов организации самостоятельной работы, как залога успешного саморазвития личности учащегося.

Актуальность работы

Наше время предъявляет к человеку свои требования. Уже недостаточно быть носителем какой то суммы знаний, необходимо в течение всей жизни уметь учиться самостоятельно, работать с большим объемом информации, постоянно перерабатывая и обновляя свои знания и умения. Человек должен уметь подходить к любому делу творчески, с интересом. Только в этом случае можно будет ожидать хороших результатов в любой области деятельности.

Общеизвестно, что учащиеся прочно усваивают только то, что прошло через их индивидуальное усилие. Проблема самостоятельности учащихся при обучении не является новой. Этому вопросу отводили исключительную роль ученые всех времен. Особенно четкие концепции о роли самостоятельности в приобретении знаний имеются в трудах К.Д.Ушинского, Н.Г.Чернышевского, Д.И.Писарева и др. Эта проблема является актуальной и сейчас.

Воспитание самостоятельности у учащихся происходит постепенно в течение всего периода обучения и предусматривает полноценно аргументировать, выделять главное, существенное, умение рассуждать, доказывать, находить рациональные пути выполнения заданий, делать соответствующие выводы, обобщать и применять их при решении конкретных вопросов. Каждый преподаватель должен обучать студентов разумной организации своей работы, методом самообразования.

Самостоятельная работа не самоцель. Она является средством борьбы за глубокие и прочные знания учащихся, средством формирования у них активности и самостоятельности как черт личности, развития их умственных способностей.

Актуальность этой проблемы бесспорна, т.к. знания, умения, убеждения, духовность нельзя передать от преподавателя к учащемуся, прибегая только к словам. Этот процесс включает в себя знакомство, восприятие, самостоятельную переработку, осознание и принятие этих умений и понятий.

Ориентация на личность с высоким уровнем сформированности различных качеств интеллекта, способную к самоопределению и свободному развитию, побуждает преподавателя к постоянному поиску путей обновления образовательного процесса, а также выявлению и созданию психолого-педагогических условий, необходимых для полного раскрытия и развития интеллектуального потенциала учащихся. Но традиционные методы обучения, содержание учебного материала, формы организации учебно-воспитательного процесса не позволяют обеспечить динамичное развитие личности учащихся.

Таким образом, обнаруживается противоречие между использованием традиционной методики преподавания с опорой на идею максимальной помощи учащимся в обучении и необходимостью повышения уровня самостоятельности учащихся в познавательной деятельности

Ведущая педагогическая идея

Ведущая педагогическая идея опыта – формирование у студентов самостоятельности, на основе двух тесно связанных между собой задач. Первая из них заключается в том, чтобы развивать у студентов самостоятельность в познавательной деятельности, учить их самостоятельно овладевать знаниями, формировать свое мировоззрение; вторая — в том, чтобы учить их самостоятельно применять имеющиеся знания в учении и практической деятельности.

Длительность работы над опытом

Работа над опытом планируется в течение трех лет с сентября 2013г. по июль 2016г.

Диапазон опыта

Диапазон данного опыта работы представлен системой работы преподавателя при организации уроков математики.

Теоретическая база опыта

Самостоятельная работа – это такая работа, которая выполняется без

непосредственного участия преподавателя, но по его заданию, в специально предоставленное для этого время, при этом учащиеся, сознательно стремятся достигнуть поставленные цели, употребляя свои усилия и выражая в той или иной форме результат умственных или физических ( либо тех и других вместе) действий.

1-й уровень. Учащиеся самостоятельно и доказательно строят один или несколько непосредственных выводов из одного исходного.

2-й уровень. Умение доказательно прийти к нескольким параллельным и изолированным друг от друга непосредственным выводам на основе нескольких различных данных.

3-й уровень. Умение сделать доказательно один или несколько опосредованных выводов из одного или нескольких данных условия, при этом все выводы должны быть изолированы друг от друга.

4-й уровень. Умение делать опосредованные выводы на основе выявления связи между различными данными условия.

Новизна опыта

Новизна опыта моей работы заключается в комбинировании элементов известных методик и технологий, способствующих развитию самостоятельности на уроках математики. Новизна опыта проявляется в отборе разноуровневых задач по математике, широком использовании методов работы с любыми источниками информации ( учебника, Интернета, справочной литературой), оригинальной компоновке учебного материала.

Раздел II

Технология опыта

Целью педагогической деятельности является обеспечение положительной динамики творческой самореализации учащихся на уроках математики, раскрытие индивидуальности студента, что создаёт благоприятные условия для формирования учебно-интеллектуальных умений и навыков, для развития самостоятельной познавательной активности, профессиональной направленности личности.

Достижение планируемых результатов предполагает решение следующих задач:

использование наряду с традиционными формами учебных занятий индивидуальных и групповых занятий в рамках внеурочной деятельности;
создание условий для приобщения студентов к самостоятельной познавательной деятельности;
использование современных приемов, средств и методов обучения, ориентированных на повышение познавательной активности студентов;
отслеживание эффективности использования применяемых приемов, средств и методов обучения.

Организация учебно–воспитательного процесса основана на использовании следующих этапов:

Этап диагностики образовательных возможностей учащихся. Осуществляется изучение индивидуальных особенностей математического мышления студентов, а также уровень интеллектуальных и творческих способностей каждого. Для этого используются специализированные тесты (Приложение 1) и задания по изученным темам разного уровня сложности.
Этап планирования и проектирования индивидуальной педагогической поддержки учащихся в процессе обучения. По каждой теме проектируется схема повторения изученного материала, что позволяет повысить уровень остаточных знаний.
Этап совместной работы преподавателя и студента по конструированию его индивидуальной образовательной траектории. Данный этап позволяет студенту спланировать свою учебную деятельность.
Этап реализации.

Изучение нового учебного материала. Сопровождается осуществлением мер по широкому использованию в учебном процессе коммуникативно– деятельностного, индивидуально-личностного и проблемного подходов.

Закрепление и комплексное применение знаний и способов действий.

Использование практикумов, учебных проектов и других видов самостоятельной работы учащихся по применению полученных знаний. Применяются групповые и индивидуальные формы работы, постепенно увеличивается уровень сложности решаемых задач, используются творческие задания для повышения креативности мышления. Задания подбираются так, чтобы студенты могли справиться с предложенной работой (самостоятельно или с помощью преподавателя), чтобы каждый студент в ходе учебных занятий оказался в ситуации успеха в соответствии с уровнем его способностей, имея возможность получить необходимую своевременную помощь.

Этап контроля и анализа результатов. В самостоятельные проверочные работы включаются задания разной сложности. Это позволяет выявить качество усвоения материала и правильность осуществленного учащимися выбора. Уровень развития учащихся отслеживается посредством балльно-рейтинговой системы оценки знаний.

В соответствии с поставленными целями и задачами педагогической деятельности в рамках представляемого опыта используются разнообразные формы, методы и средства учебно-воспитательной работы.

В теории и практике обучения наиболее распространены следующие подходы к классификации самостоятельных работ:

по дидактическим целям (обучающие, контролирующие, развивающие);

по уровню самостоятельности учащихся (по образцу, реконструктивно-вариативные, частично-поисковые (эвристические), исследовательские (творческие));

по степени индивидуализации (классные, групповые и индивидуальные);

по источнику и методу приобретения знаний (работа с книгой, решение и составление задач, лабораторные и практические работы, подготовка докладов, рефератов и т.д.)

по форме выполнения (устные и письменные самостоятельные работы);

по месту выполнения (классные и домашние).

Рассмотрим некоторые виды самостоятельных работ и их сочетание более подробно.

Классификация по степени индивидуализации включает общеклассные, групповые и индивидуальные самостоятельные работы. Их проводят, в той или иной мере учитывая индивидуальные особенности каждого ученика, в условиях органического соединения индивидуальной и коллективной деятельности учащихся.

Самостоятельные работы по дидактическому назначению можно разделить на обучающие, контролирующие и развивающие.

Обучающие работы предназначены для организации самостоятельной деятельности учащихся, ориентированной на усвоение знаний и выработку умений применять их. Они часто носят индивидуальный характер и предназначены для ребят, по тем или иным причинам, не усвоившим материал вместе с остальной частью класса. Обучающие самостоятельные работы в свою очередь подразделяют на работы по формированию знаний и работы по формированию умений. Во всех случаях надо стремиться проводить обучающие работы в непринужденной, деловой обстановке, чтобы ребята не боялись задавать любые вопросы, были бы уверены, что за ошибки их не накажут, а там, где требуется, помогут, покажут, повторно разъяснят. (Приложение 2)

Развивающие самостоятельные работы даются либо индивидуально каждому ученику, либо всему классу сразу с целью привлечения внимания к нестандартным заданиям, которые способствуют развитию логического мышления. Такие задания полезно давать ученикам в качестве домашней работы. На уроках развивающим задачам обычно отводят немного времени и предлагают ученикам в конце урока, если остается время после изучения запланированного материала, либо в начале, в качестве разминки. Если систематически уделять 5-10 минут урока таким задачам результаты не заставят себя ждать.

Например:

1. Найти сходство (общие признаки, свойства, характеристики) у разных геометрических объектов (у ромба и прямоугольника; треугольника и трапеции; окружности и сферы; смежных углов и вертикальных углов и т. д.).

2. а) Перечислить как можно больше геометрических объектов с данным свойством (имеет прямой угол; содержит 4 отрезка; диагонали точкой пересечения делятся пополам; можно вписать окружность). б) Перечислить как можно больше предметов, обладающих несколькими заданными свойствами (имеет прямой угол и острый; имеет два равных угла).

Развивающими являются самостоятельные работы с переадресацией цели. Например, задания с кодами. На урок задаются примеры, решая которые студент получает ответ. Все ответы и посторонние значения заносятся в таблицу, где напротив значения указана буква или слог. Из полученных ответов-букв (слогов) складываются слова или предложения.

Контролирующие самостоятельные работы призваны проверить степень усвоения материала для своевременной коррекции знаний и накопления оценок. Нередко со всеми учащимися группы проводятся двух и более вариантные самостоятельные работы, идентичные по содержанию. Ныне же все большее применение получают дифференцированные самостоятельные работы, соответствующие разному уровню подготовленности учащихся одной и той же группы. Обычно в практике обучения используются до 8 вариантов разноуровневых заданий.

В практике для развития самостоятельности мышления, преподаватель использует самостоятельные и контрольные работы не менее чем в четырех вариантах. В зависимости от степени сложности темы, работы дифференцируются по уровням сложности. Обычно применяет 2 уровня сложности, реже три. К первому, более легкому уровню, часто прилагается справочный материал, опорные формулы. (Приложение3)

Одним из видов самостоятельных ра6от, являются работы в которых дифференцирована лишь помощь, оказываемая учащимся. Основу такой работы составляют одни и те же задания. Варьируется только система указаний для групп учащихся с различным уровнем подготовленности. Такие работы называют многовариативными. Степень подсказок может быть разной, вплоть до заполнения пропусков необходимыми вычислениями. (Приложение 4)

При выполнении самостоятельных работ по образцу учащиеся не выходят за рамки воспроизводящей деятельности, которая направлена на овладение основными знаниями, умениями, способами работы. Предлагаемые при этом задания выполняются по образцам и алгоритмам, показанным учителем или подробно описанным в учебнике. Они играют важную роль при первичном закреплении изученного, ибо способствуют созданию условий для перехода учащихся к выполнению заданий, требующих более высокого уровня самостоятельности. Поэтому преподаватель должен уметь отбирать, вовремя предъявлять и требовать от учащихся их точного воспроизведения.

Самостоятельные работы реконструктивно-вариативного вида обычно содержат в себе задачи, по условиям которых учащимся приходится анализировать новые для них ситуации, переформулировать их, выбирать из известных способов наиболее рациональные. Они отличаются от работ по образцу тем, что при их выполнении необходимо преобразовать исходные данные, т.е. проявить более высокий уровень самостоятельности.
(Приложение 5)

Еще более высокий уровень самостоятельности учащиеся проявляют при выполнении частично-поисковых (эвристических) работ, требующих переноса знаний и умений в необычные, нестандартные ситуации. Высшая степень самостоятельности учащихся проявляется при выполнении исследовательских (творческих) самостоятельных работ. Здесь, пользуясь накопленными знаниями и умениями, выдвигая и проверяя собственные гипотезы и суждения, они учатся открывать для себя новые сведения об изучаемых объектах. Такие задачи обладают наибольшим развивающим потенциалом. Полезно сначала задавать подобные самостоятельные работы на дом, чтобы ребенок мог попробовать решить задачу без помощи учителя, вникнуть в суть, предложить свой способ решения, а уже затем обсудить решение всем коллективом. Обычно эвристические задачи используются при проведении олимпиад, турниров, конкурсов.

Самостоятельные работы разных типов и видов с большим или малым количеством вариантов призваны обеспечить индивидуализацию обучения, его гуманизацию. Они направлены в первую очередь на развитие познавательной самостоятельности ребенка, которая очень необходима для жизни в современном информационном обществе. Совершенствование методики преподавания и методов обучения неразрывно связано с вопросами развития самостоятельности у учащихся. Поэтому использую различные приемы работы с учеником. На занятиях ориентируюсь на всех учащихся в целом и на каждого в отдельности, имея в виду общие знания. Считаю, что такой подход побуждает к работе слабого ученика и стимулирует сильного.

Для этого выбираю разные методы работы: устный; словесно-графический; наглядный; практический.

Каждый из них реализуется в системе приемов, таких как: фронтальный опрос, устные контрольные работы, построение графиков, диаграмм, фигур на плоскости и в пространстве, работа с ними, с перфокартами, моделями по алгоритму, практические и лабораторные, работа над проектами, сказками, рефератами.

Использую дифференцированные средства обучения: таблицы, учебник, схемы, модели фигур и плоскостей, проекты, описание работ, чертежные и измерительные приборы, карточки для устной и письменной работы, дополнительную и справочную литературу.

Наша жизнь не стоит на месте. С улучшением материальной базы ОУ применение компьютеров, информационных ресурсов на уроках даёт преподавателю новые возможности реализации себя и своих задумок. Применение на уроках медиалекций, интерактивных карт, игр, моделей, видеофрагментов, графиков, тренажёров переводит образование на более высокую и качественную ступень.

Из всего выше изложенного можно сделать следующий вывод. Самостоятельная работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала. При тщательно продуманной методике проведения самостоятельных работ ускоряются темпы формирования у студентов умений и навыков практического характера, а это в свою очередь оказывает положительное влияние на формирование познавательных умений и навыков. С течением времени при систематической организации самостоятельной работы на уроках и сочетании её с различными видами домашней работы по математики у учащихся вырабатываются устойчивые навыки самостоятельной работы. В результате для выполнения примерно одинаковых по объёму и степени трудности работ учащиеся затрачивают значительно меньше времени по сравнению с учащимися таких группах, в которых самостоятельная работа совершенно не организуется или проводится нерегулярно. Это позволяет постепенно наращивать темпы изучения программного материала, увеличить время на выполнение заданий различного типа, выполнение исследовательских работ и других видов работ творческого характера.

Раздел III

Результативность опыта

	Компонент познавательной самостоятельности
Уровень	Мотивационный	Волевой	Содержательно-операционный
Репродуктивный	95%	5%	2%
Частично-поисковый	5%	5%	4%
Исследовательский	0%	0%	0%

Результаты данного опыта выражаются в уровне самостоятельности учащихся, в положительной динамике творческого саморазвития учащихся на уроках математики, в развитии самостоятельной познавательной активности.

Результаты сформированности
уровней познавательной самостоятельности учащихся 9 класса.

Библиографический список:

Агапов Е.М. Индивидуальная работа с учащимися на уроках математики. – М., Просвещение, 1999.
Бабанский Ю.К. Оптимизация процесса обучения.-М.: Педагогика,
Бухвалов В.А. Развитие учащихся в процессе творчества и сотрудничества. - М., Центр "Педагогический поиск". - 2000г.
Горностаева З.Я “Проблема самостоятельной познавательной деятельности”, Открыт. школа. – 1998. - №2
Гусев В.А. Индивидуализация учебной деятельности учащихся как основа дифференцированного обучения математике в средней школе.- Математика в школе.-1990.-№4.
Жарова Л.В. “Управление самостоятельной деятельностью учащихся” - Ленинград, -1982.
Калмыкова З.И. Психологические принципы развивающего обучения.- М.: Знание, 1979.-126с.
Лернер И.Я. Критерии уровней познавательной самостоятельности учащихся // Новые исследования в педагогических науках. – М.: Педагогика, 1971. – №4. – С.34-39.
Математика. Дидактические материалы. 7-11 класс. 2006-2007г.г.
Мудрая Л.З. Организация индивидуальной работы учащихся на уроках математики. – М., Высшая школа, 1975.
Ромашко И.В., Винник В.М. Технология работы в разноуровневых группах.- Математика в школе.-1996, №4.-с.40-41.
Рыжова В.Н. Дифференциация обучения как важный фактор развития познавательных интересов школьников. - Научно-практический журнал "Завуч" - 2003г., № 8.
Тимощук М.Е. О дифференцированной помощи учащимся при решении задач-Математика в школе.1990.№3.-с.13-15
Унт И.Э. Индивидуализация и дифференциация обучения.- М.:Педагогика,1990. -191с.
Утеева Р.А. Дифференцированные формы учебной деятельности учащихся.- Математика в школе,№5-с.32-33.
Черникова Т.М. Уроки в парах сменного состава.-Математика в школе.-1995, № 2.-с.45-46.
Шамова Т.И. Активизация учения школьников. – М.:Педагогика, 1982. – 208с.
Якиманская И.С. Личностно-ориентированное обучение в современной школе. - М.:-Сентябрь,1996.-96с.

Приложения

1.Приложение1-Тесты изучение индивидуальных особенностей
математического мышления студентов.

2. Приложение 2- Обучающие самостоятельные работы.

3. Приложение 3- Контрольные работы не менее чем в четырех вариантах.

4. Приложение 4- Многовариативные самостоятельные работы.

5. Приложение 5- Разработка урока алгебры по теме «Нахождение свойств функций по формуле и по графику».

6. Приложение 6 -Критерии сформированности уровней познавательной самостоятельности учащихся по Т.И. Шамовой.

Приложение №1

Тесты изучение индивидуальных особенностей
математического мышления учащихся

Методика "Логическое мышление"

Цель:

Выявить наличие или отсутствие у студентов умения оперировать с логическими элементами.

Ход эксперимента:

Учитель предлагает ученикам задание, где из двух истинных утверждений необходимо сделать заключение об истинности, ложности или неопределенности третьего утверждения.

Задания:

Все десятичные дроби - числа.
1,5 - десятичная дробь.
1,5 - число?
Если число оканчивается нулем или цифрой 5, то оно делится на 5.
Число 435 оканчивается цифрой 5.
Число 435 делится на 5?
Некоторые люди обладают способностью к быстрому и точному счету.
Некоторые люди - математики.
Следовательно, все математики обладают способностью к быстрому и точному счету?
-8 - отрицательное число.
-8 - целое число.
Следовательно, все целые числа являются отрицательными числами?
Все натуральные числа - рациональные.
Нечетные числа - натуральные.
Следовательно, нечетные числа - рациональные?

Методика "Выделение существенных признаков математических понятий"

Цель:

Определить умение выделять существенные признаки математических понятий.

Ход эксперимента:

Преподаватель предлагает ученикам ряд математических терминов. Ученикам необходимо выбрать из пяти предложенных математических терминов два, которые наиболее точно определяют математическое понятие.

Задания:

Уравнение (корень, равенство, сумма, неизвестная, произведение);
Сумма (слагаемое, равенство, плюс, делитель, множитель);
Периметр (разность, сторона, сумма, фигура, прямоугольник);
Дробь (делимое, числитель, частное, знаменатель, произведение);
Координата (плоскость, абсцисса, ось, ордината, прямая).

Правильные ответы задания выделены курсивом.

Методика "Исключение лишнего"

Цель:

Определение способности к обобщению.

Ход экперимента:

Учитель предлагает ученикам ряд математических понятий или чисел, математических выражений. В каждом из заданий пять элементов, четыре из которых обладают общим свойством, а пятый не обладает этим свойством. Ученикам необходимо исключить элемент, не относящийся к группе других элементов, и объяснить, почему он это сделал.

Задания:

8; 20; -4; 18; 5.
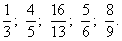
Делимое, частное, плюс, деление, делитель.
Точка, отрезок, прямая, уравнение, плоскость.
Координата, ось, абсцисса, фигура, ордината.

Задание № 1
"Аналогия"

Вам предлагается три слова. Между первым и вторым словами существует определенная связь. Между третьим словом и одним из пяти предложенных существует такая же связь. Это слово Вам предстоит найти.

Пример: песня - композитор - самолет - ?

а) аэропорт; б) полет; в) конструктор; г) горючее; д) истребитель.

Ответ: "конструктор", надо вынести букву "в".

Слагаемое - сумма = множители - ?
а) разность; б) делитель; в) произведение; г) умножение; д) число.
Фигура - треугольник = состояние вещества - ?
а) жидкость; б) движение; в) температура; г) вода; д) молекула.
Прямоугольник - плоскость = куб - ?
а) пространство; б) ребро; в) высота; г) треугольник; д) сторона.
Диаметр - радиус = окружность - ?
а) дуга; б) сегмент; в) отрезок; г) линия; д) круг.

Задание № 4
"Числовые ряды"

Предлагаем ряды чисел, расположенных по определенному правилу. Ваша задача состоит в том, чтобы определить число, которое было бы продолжением соответствующего ряда. Напишите его под соответствующим номером в задании № 4 опросника.

Пример: 2, 4, 6, 8, 10... В этом ряду каждое последующее число на 2 больше предыдущего, поэтому следует написать число 12.

1	6	9	12	15	18	21	... ?
2	9	1	7	1	5	1	... ?
3	2	3	5	6	8	9	... ?
4	10	12	9	11	8	10	... ?
5	1	3	6	8	16	18	... ?
6	3	4	6	9	13	18	... ?
7	15	13	16	12	17	11	... ?
8	1	2	4	8	16	32	... ?
9	1	2	5	10	17	26	... ?
10	1	4	9	16	25	36	... ?
11	1	2	6	15	31	56	... ?
12	31	24	18	13	9	6	... ?
13	174	171	57	54	18	15	... ?
14	54	19	18	14	6	9	... ?
15	301	294	49	44	11	8	... ?

"Сложная аналогия"
Образец

Овца - стадо.
Малина - ягода.
Море - океан.
Свет - темнота.
Отравление - смерть.
Враг - неприятель.

Найти общее в соответствии 16 пар слов со словами, данными в качестве образца. Поставить перед каждой парой цифру соответствующего образца.

1. Испуг - бегство.	9. Свобода - независимость.
2. Математика - наука.	10. Месть - поджог.
3. Правильно - верно.	11. Десять - число.
4. Грядка - огород.	12. Праздность - безделье.
5. Похвала - брань.	13. Глава - роман.
6. Пара - два.	14. Покой - движение
7. Слово - фраза.	15. Бережливость - скупость
8. Бодрость - вялость.	16. Прохлада - мороз.

Ключ
1 - 5	5 - 4	9 - 6	13 -3
2 - 2	6 - 6	10 - 5	14 - 4
3 - 6	7 - 1	11 - 2	15 - 3
4 - 1	8 - 4	12 - 6	16 - 3

"Выделение существенных признаков"

Стереометрия (фигура, пирамида, пространство, перпендикуляр, вектор).
Куб (угол, равенство, плоскость, чертеж, грань).
Координата (аппликата, прямая, плоскость, ось, ордината).
Кольцо (алмаз, диаметр, проба, круглость, печать).