«ФИНАНСОВАЯ ГРАМОТНОСТЬ
НА УРОКАХ ИНФОРМАТИКИ ИЛИ
КАК НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ
НА ВЫИГРЫШНУЮ СТРАТЕГИЮ (19,20,21)»
Мой анализ
Баллы от 1 до 10
16 декабря 2020
Вопросы встречи
- Кто планирует свой день?
- Кто и как инвестирует в свое будущее?
- Когда этим надо заниматься?
- Что такое инвестиции?
- Как построить зависимость вашего времени и эффективности выполненных дел?
- Знания, их накопление – это инвестиции?
- Какой результат на ЕГЭ по информатике планирую получить?
- Как часто я решаю задачи ЕГЭ и сколько вопросов я задаю учителю на уроках информатики?
« ФИНАНСОВАЯ ГРАМОТНОСТЬ
НА УРОКАХ ИНФОРМАТИКИ
ИЛИ
КАК НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ
НА ВЫИГРЫШНУЮ СТРАТЕГИЮ (19,20,21)»
ЕГЭ
2021
- Инвестиции – это размещение какого-либо ресурса с целью получения прибыли.
- Интеллектуальные инвестиции — это инвестиции, вкладываемые в создание интеллектуального продукта , т.е. вложения средств в создание новых нематериальных активов, а также в обучение персонала и повышение его квалификации для создания в дальнейшем инновационных продуктов.
ВЫИГРЫШНАЯ СТРАТЕГИЯ - задачи ЕГЭ №№19,20,21
Вариант 15 - №19
- Два инвестора , Петя и Ваня, начинают инвестировать в новый проект.
- Перед инвесторами – проект с начальным капиталом S. Инвесторы совершают сделки по очереди, первый ход делает Петя.
- За один ход инвестор может добавить в проект один миллион рублей или два миллиона рублей или увеличить количество инвестиций в проект в два раза.
- Проект завершается в тот момент, когда количество капитала в проекте становится не менее 40 миллионов рублей. Победителем проекта считается инвестор, сделавший последний ход, то есть первым получивший инвестиционный проект, в котором будет 40 или более миллионов рублей.
- В начальный момент в проекте находился капитал - S, 1 ≤ S ≤ 39.
- Будем говорить, что инвестор имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
- Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S , когда такая ситуация возможна .
- Задание 19 №
- Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней . Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
- Игра завершается в тот момент, когда количество камней в куче становится не менее 40. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 40 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 39.
- Будем говорить, что игрок имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
- Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети . Укажите минимальное значение S , когда такая ситуация возможна.
Ответ:
=40 1)+1 2)+2 3)*2 Задача двухходовая П-В П В =40 *2 *2" width="640"
Решение 15-№19
Решение 15-№19
S=40
1)+1
2)+2
3)*2
- Задача двухходовая П-В
П
В
=40
*2
*2
- 40/4=10
Вариант 15- №20
Два инвестора, Петя и Ваня, начинают инвестировать в новый проект.
Перед инвесторами – проект с начальным капиталом S. Инвесторы совершают сделки по очереди, первый ход делает Петя.
За один ход инвестор может добавить в проект один миллион рублей или два миллиона рублей или увеличить количество инвестиций в проект в два раза.
Проект завершается в тот момент, когда количество капитала в проекте становится не менее 40 миллионов рублей. Победителем проекта считается инвестор, сделавший последний ход, то есть первым получивший инвестиционный проект, в котором будет 40 или более миллионов рублей.
В начальный момент в проекте находился капитал - S, 1 ≤ S ≤ 39.
Будем говорить, что инвестор имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Найдите два таких значения S , при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
=40 1)+1 Задача трехходовая П-В-П 2)+2 3)*2 18 17 19 20 В П П =40 +1 *2 ? Нужна стратегия, по опыту первой задачи (19) Петя не будет *2. Ответ: 1718" width="640"
Решение 15-№20
S=40
1)+1
- Задача трехходовая П-В-П
2)+2
3)*2
18 17
19
20
В
П
П
=40
+1
*2
?
Нужна стратегия, по опыту первой задачи (19) Петя не будет *2.
Ответ: 1718
=40 Задача четырехходовая П-В-П-В Найдите минимальное значение S , при котором одновременно выполняются два условия: — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; — у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. 18 17 19 20 ? В П В П *2 =40 +1 ? +1 Нужна стратегия Ване, по опыту первой задачи (19) Ваня не будет *2. Ответ: ____" width="640"
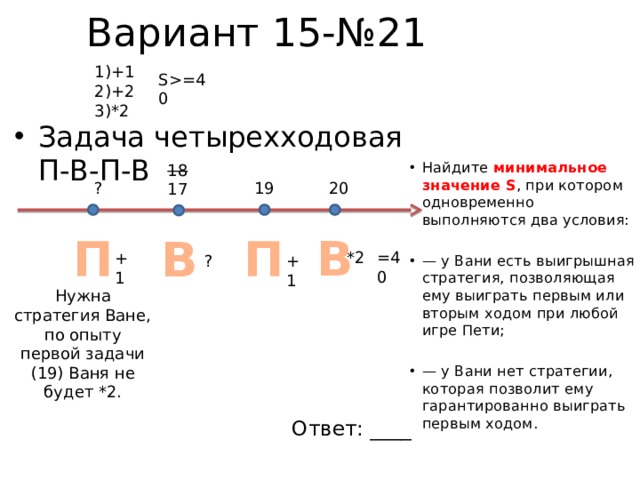
Вариант 15-№21
1)+1
2)+2
3)*2
S=40
- Задача четырехходовая П-В-П-В
- Найдите минимальное значение S , при котором одновременно выполняются два условия:
- — у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- — у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
18 17
19
20
?
В
П
В
П
*2
=40
+1
?
+1
Нужна стратегия Ване, по опыту первой задачи (19) Ваня не будет *2.
Ответ: ____
Задание 19 № 28062
Вариант 14
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 31 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 30.
Будем говорить, что игрок имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S , когда такая ситуация возможна.
Ответ:
1)+1
2)+2
3)*2
S=31
В
П
=31
*2
*2
31/4 с избытком, чтобы победил Ваня
__
?
16
Задание 20 № 28063
Найдите два таких значения S , при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Ответ:
П
П
В
=31
*2
?
+1
Задание 21 № 28064
Найдите минимальное значение S , при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответ:
В
П
П
В
*2
=31
+1
?
+1
Вариант 1
Задание 19 № 27754
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза . Например, пусть в одной куче 6 камней, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (7, 9), (24, 9), (6, 10), (6, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 61. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 61 или больше камней.
В начальный момент в первой куче было 3 камня, во второй куче — S камней, 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, то есть не гарантируют выигрыш независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S , когда такая ситуация возможна.
Ответ:
1)+1
S 1 +S 2 =61
3+S=61
2)*4
S=58
В
П
=58
*4
*4
58/16 с избытком, чтобы победил Ваня
=61 3+S=61 2)*4 S=58 В П П ? +1 *4 S 1 +S 2 =61 1)+1 3+S=61 2)*4 S=58 В П В П ? +1 +1 *4" width="640"
Вариант 1
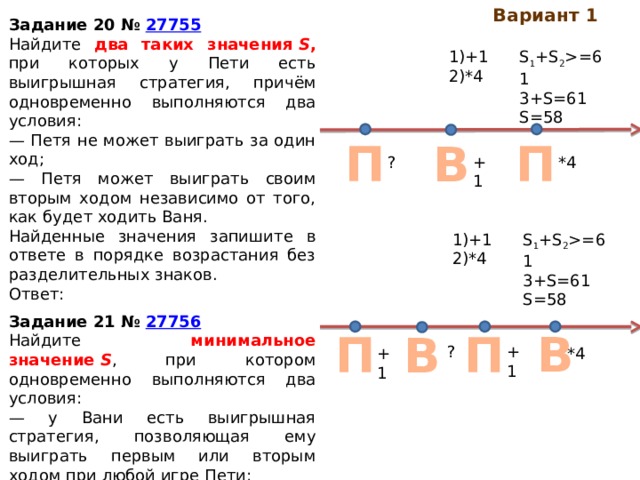
Задание 20 № 27755
Найдите два таких значения S , при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Ответ:
Задание 21 № 27756
Найдите минимальное значение S , при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответ:
1)+1
S 1 +S 2 =61
3+S=61
2)*4
S=58
В
П
П
?
+1
*4
S 1 +S 2 =61
1)+1
3+S=61
2)*4
S=58
В
П
В
П
?
+1
+1
*4
Решение вариант 1 – 20-21
Ваня пытается победить, но ему не хватает 1 балла
4+4S=60
4S=56
S=14
(4,S)
+1
(3,S)
*4
(12,S)
Ваня пытается победить, но ему не хватает 1 балла
12+4S=60
4S=48
S=12
Стратегия Пети: ходить с меньшей кучи.
=61 3+S=61 2)*4 S=58 В П П ? +1 *4 S 1 +S 2 =61 1)+1 3+S=61 2)*4 S=58 В П В П ? +1 +1 *4" width="640"
Вариант 1
Задание 20 № 27755
Найдите два таких значения S , при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
Ответ:
Задание 21 № 27756
Найдите минимальное значение S , при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответ:
1)+1
S 1 +S 2 =61
3+S=61
2)*4
S=58
В
П
П
?
+1
*4
S 1 +S 2 =61
1)+1
3+S=61
2)*4
S=58
В
П
В
П
?
+1
+1
*4
10. Будем говорить, что игрок имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т. е не гарантирующие выигрыш независимо от игры противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите максимальное значение S , когда такая ситуация возможна. Ответ: 1)-1 S 1 +S 2 10+S=20 2):2 S=10 П В =10 :2 :2 S max - ?" width="640"
Профильное задание Вариант 2 - №19
Задание 19 № 27771
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень меньше, чем убирается). Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 4).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней.
В начальный момент в первой куче было 10 камней, во второй куче — S камней, S 10.
Будем говорить, что игрок имеет выигрышную стратегию , если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по ней игрока, которые не являются для него безусловно выигрышными, т. е не гарантирующие выигрыш независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите максимальное значение S , когда такая ситуация возможна.
Ответ:
1)-1
S 1 +S 2
10+S=20
2):2
S=10
П
В
=10
:2
:2
S max - ?
«ФИНАНСОВАЯ ГРАМОТНОСТЬ
НА УРОКАХ ИНФОРМАТИКИ ИЛИ
КАК НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ
НА ВЫИГРЫШНУЮ СТРАТЕГИЮ (19,20,21)»
Мой анализ
Баллы от 1 до 10
16 декабря 2020
Итоги встречи
- Я планирую свой день.
- Я инвестирую в свое будущее.
- Я сконцентрирован на подготовке к ЕГЭ.
- Я с каждым днем увеличиваю свой интеллектуальный инвестиционный портфель.
- Я эффективно строю зависимость моего времени и выполненных дел.
- Знания, их накопление – это мои инвестиции.
- Я анализирую свои успехи для достижения результата на ЕГЭ по информатике.
- Я решаю задачи ЕГЭ и составляю список вопросов, на которые я могу найти ответ на уроках информатики?
Наш инвестиционный портфель пополнился.
Желаю всем быть успешными инвесторами своей жизни.
