КАРТОЧКА № 1.
Уравнение касательной к графику функции у=f(x) точке (х0 ; у0)
Уравнение касательной к графику функции у=f(x) точке (х0 ; у0),
имеет вид ук= f(x0) + f/(x)(х- х0).
Задание. Напишите уравнение касательной к графику функции у=f(x) в точке с абсциссой x0 =1, если f(x)=х3+2х2-5.
| № | План составления уравнения касательной к графику функции у=f(x) в заданной точке | Применение плана |
| 1 | Вычисляем значение функции в точке х= х0 | x0 =1, у0= f(1), у0=1+2-5=-2 |
| 2 | Находим производную функции f/(x) | f/(x)=3х2+4х |
| 3 | Вычисляем значение производной функции в точке x0, т.е. f/(x0) | f/(x0)= f/(1)=3+4=7 |
| 4 | Подставляем значения в уравнение касательной ук= f(x0) + f/(x)(х- х0). | ук= f(x0) + f/(x)(х- х0) ук=-2+7(х- 1), ук= 7х-9 |
| 5 | Записываем ответ. | Ответ: ук= 7х-9 |
Примеры. Применяя указанный выше план, напишите уравнение касательной к графику функции у=f(x) точке х0, если
f(x)= 1-х2 , х0=1;
f(x)= х3-2х, х0= -1;
f(x)=sin3x, х0=П/3.
КАРТОЧКА № 2.
Наименьшее и наибольшее значения функции.
Задание. Найдите наименьшее и наибольшее значения функции у= х4-2х2-3 на промежутке [0;2].
| № | План нахождения унаим и унаиб на [0;2]. | Применение плана |
| 1 | Находим производную функции | у/= 4х3-4х=4х(х2-1) |
| 2 | Находим стационарные точки функции | у/=0, 4х (х2-1)=0, х=0, х=1, х=-1 -стационарные точки |
| 3 | Выбираем стационарные точки, лежащие внутри [а;в]. | 0 |
| 4 | Находим значения функции в стационарных точках (внутри данного отрезка) и на концах отрезка | у(1) =1-2-3=-4, у(0)=-3 , у(2)=16-8-3=5 . |
| 5 | Из найденных значений функции выбираем наименьшее и наибольшее | унаим = у(1) =-4) унаиб=у(2)=5 |
| 6 | Записываем ответ | Ответ: унаим =-4) унаиб=5 . |
Примеры. Применяя указанный выше план, найдите наименьшее и наибольшее значения функции у=f(x) на промежутке [а;в], если:
f(x)=3х2-х3, [-1;3];
f(x)=- 3х2+х3+3х+2, [-2;2];
f(x)=tgx+ctg2x, [П/6; П/3];
f(x)= 2х2-lnx, [1;е]
f(x)=- 3х2+х3+3х+2, (-2;2).
КАРТОЧКА № 3. Исследование функции на монотонность и экстремумы
Задание. Исследуйте функцию f(x) = 3х4-4х3+1 на монотонность и экстремумы.
| № | План | Применение плана |
| | Найти область определения и интервалы, на которых функция непрерывна. | Область определения: x Функция непрерывна в каждой точке своей области определения |
| | Найти производную f/(х) | f/(х)=12х3-12х2=12х2(х-1) |
| | Найти критические точки, т.е. внутренние точки области определения, в которых f/(х)=0 или не существует | f/(х) существует на всей области определения. f/(х)=0 при х=0, х=1 |
| | Отметить критические точки на области определения; найти знак производной и характер поведения функции на каждом из интервалов, на которые разбивается область определения |
|
| | Относительно каждой критической точки определить, является ли она точкой максимума или не является точка экстремума | |
| | Записываем ответ исследования (промежутки монотонности и экстремумы) | Ответ: f(x) возрастает при х f(x) убывает при х уmах= f(0)=1; уmin = f(1)=0. |
КАРТОЧКА № 4. Исследование функции с помощью производной и построение ее графика
Задание. Исследуйте с помощью производной и постройте график функции 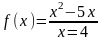 .
.
№
План
Применение плана
Найти область определения и интервалы, на которых функция непрерывна.
Область определения: 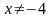
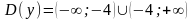
Исследовать на четность (нечетность), периодичность
Функция ни четная, ни нечетная и непериодическая.
Точки пересечения с осями координат (если можно)
Оу: х=0, у=0.
Ох: у=0, 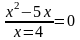 ;
; 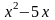 =0; х=о или х=5.
=0; х=о или х=5.
Найти производную f/(х)
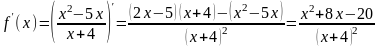
Найти критические точки, т.е. внутренние точки области определения, в которых f/(х)=0 или не существует
f/(х)=0, 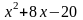 =0, при х=-10, х=2
=0, при х=-10, х=2
Промежутки возрастания и убывания, точки экстремума(и значения функции в этих точках)
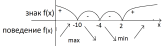
Нахождение асимптот (вертикальные, горизонтальные)
х=4 –вертикальная асимптота.
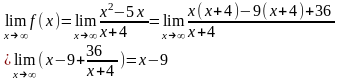 Прямая у=х-9 – наклонная асимптота
Прямая у=х-9 – наклонная асимптота
Если необходимо, найти координаты дополнительных точек, уточняющих поведение графика функции
| Х | -6 | -2 |
| у | -33 | 7 |
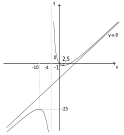
На основании проведенного исследования построить эскиз графика функции у=f(x)

 [0;2], 1
[0;2], 1 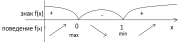
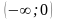 и х
и х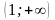
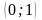 ; х
; х



