Тригонометриялық функциялардың графигі мен қасиеттері

Сабақтың тақырыбы: Тригонометриялық функциялардың

графигі мен қасиеттері

Сабақтың мақсаты:

Білімділігі: Оқушыларды тригонометриялық функциялардың графигін салу арқылы қасиеттерімен таныстыру.Есеп шығаруда қолдана білуге үйрету

Дамытушылығы: Оқушының график салу шеберлігін қалыптастыру және практикамен ұштастыруға үйрету,шығармашылығын және ойлау қабілетін дамыту

Тәрбиелігі: Оқушыны графикті тануға үйрету,ұқыпты тыңдауға ,сұрақтарға нақты жауап беруге баулу

Көрнекілігі: Компьютер , Bидеопроектор, Карточка,Слайдтар

Типі: Жаңа сабақты меңгерту

Түрі: Аралас сабақ

Жаңа технология: Компьютерлік, дамыта оқыту технологиясы

Пән аралық байланысы: Информатика

Пайдаланылған әдебиеттер:

1. 10 сынып Алгебра және анализ бастамалары,

2. « Информатика негіздері» журналы №3,2006ж

3.Интернет желісі

4. «Математика және физика» журналы

Барысы:

1. Ұйымдастыру : Оқушыны түгендеу, сабаққа даярлау

2. Үй берілген тапсырманы аралай жүріп тексеру, сұрақ қою арқылы жауап алу

3. Өткен сабақ бойынша алған білімдерін бақылау (тест сұрақтары бойынша )

4. Жаңа сабақты меңгерту

5. Есептер шығару

6. Бекіту

7. Үйге тапсырма беру

II.Үй тапсырмасы:

№70 есеп

ә) cos45⁰cos15⁰= [cos(45⁰+15⁰)+cos(45⁰-15⁰)]=[cos60⁰+cos30⁰]=

= [+]=;

№72

Б) sin(x+α)sin(x-α)=[cos(x+ α-x+ α)-cos(x+α+ x-α)]= [cos2α-cos2x]

III. Видеопроекторды қолдана отырып

бүгінгі сабақта негізгі тригонометриялық функциялардың қасиеттерін меңгеріп , қарапайым түрлендірулер көмегімен олардың графигін салудың алгоритмін қолдана отырып тригонометриялық функциялардың графиктерін салуды қарастырамыз.

Енді у=sinx , у=cosx тригонoметриялық функцияның графигін салуға тоқталайық

Слайдтан

№1

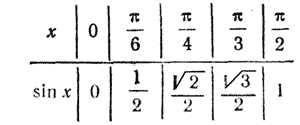
№2 у = sin х.

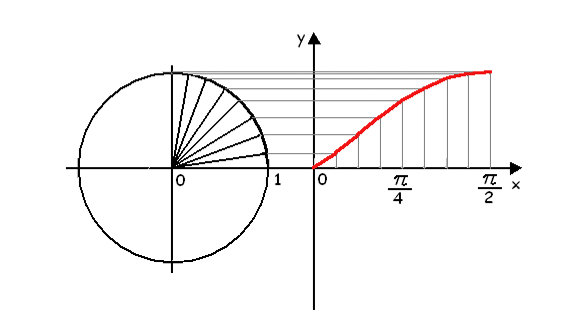
№3 у = sin х.

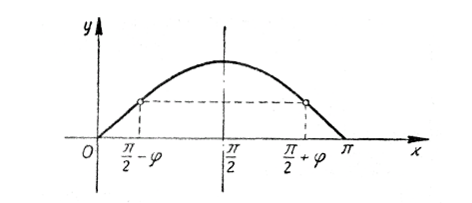
№4 Функцияның тақтығы

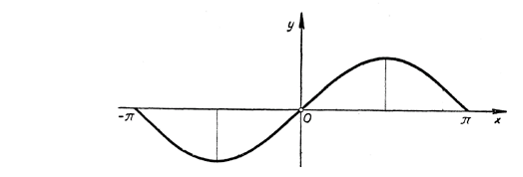
№5 Функцияның периодтылығы

№6 Синусоида қисығы

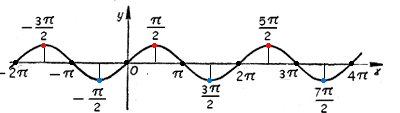
1. Функцияның анықталу облысы х€R.

2. Мәндер жиыны [-1;1]

3. sin(x+2π)=sinx, функция периодты, себебі оның ең кіші периоды 2π.

4. Функция тақ , sin(-x)=-sinx

5. [-π/2+2πk; π/2+2πk] кесінділерінде бір сарынды өспелі

[π/2+2πk; 3π/2+2πk] кесінділерінде бір сарынды кемімелі

У=sinx функциясының графигін синусоида қысығы деп атайды.

2.   y= cos x функциясын Ехcel программасының мүмкіндіктерін пайдалана отырып кесте құрып графигін саламыз .  cos х = sin (х + ^π/₂).

x=0; қадам 0,2, кесте құрып, Еxcel де графиктік диаграмманы таңдаймыз

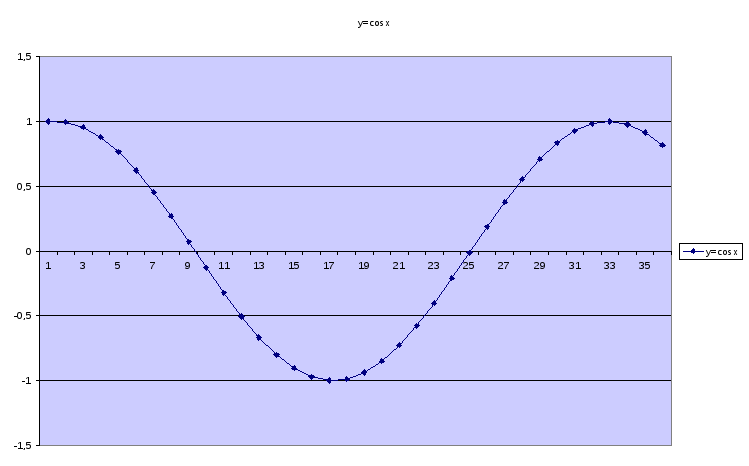
1.Функцияның анықталу облысы х€R.

2. Мәндер жиыны [-1;1]

3. cos(x+2π)=cosx, функция периодты, себебі оның ең кіші периоды 2π.

4.Функция жұп , cos (-x)=cosx

5.[-π+2πk; 2πk] кесінділерінде бір сарынды өспелі

[2πk; π+2πk] кесінділерінде бірсарынды кемімелі

У=cosx функциясының графигін косинусоида қысығы деп атайды

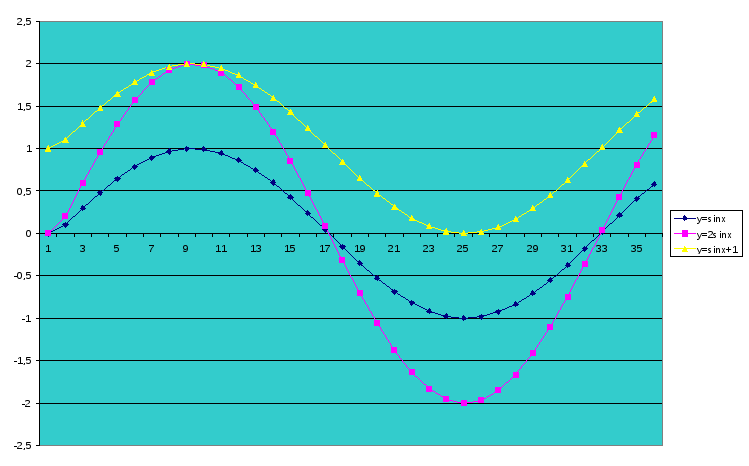
Тригонометриялық функциялардың графиктеріне қарапайым түрлендірулер қолдануға мысалдар

У=sinx

У= 2sinx

Y=sinx+1

1. Есептер шығару

А тобы.

№80 Функцияның жұптығын немесе тақтығын анықтаңдар:

1. Y=xcosx

F(-x)=-xcos(-x)=-xcosx жұп та,тақ та емес

1. Y=sin²x/x²-1

F(x)=sin²(-x)/(-x)² -1=sin²x/x²-1 жұп функция

№81 В тобы бойынша

Функциялардың графигін салыңдар У=sinx , y= cos x функцияларының графиктерін салыңдар

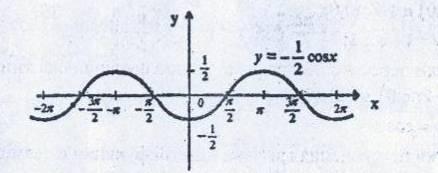
А) y=-cosx

D(y)=R cosx €[-1:1]., E(y)=

X	-2π	-	-π	-π/2	0	π/2	π		2π
y=-cosx	-1/2	0	1/2	0	1/2	0	1/2	0	-1/2

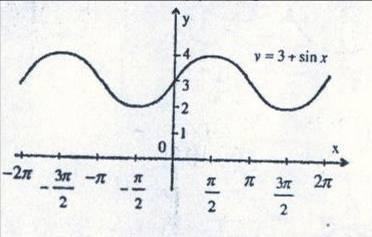
Ә) y=3+sinx

D(y)=R ,E(y)=[2;4]

sinx €[-1:1]

X	2π	-	-π	-π/2	0	π/2	π		2π
y=3+sinx	3	4	3	2	3	4	3	2	3

№82 T саны y=f(x) функциясының периоды екенін дәлелдеңдер

А) f(x) = sin, Т=8π;

Т= 2π/=8π

Ә) f(x) = 4сos2x. T=π

T=2π/2=π

№83 берілген функцияның жұп , тақ немесе жұп та ,тақ та емес екенін көрсетіңдер

а) у=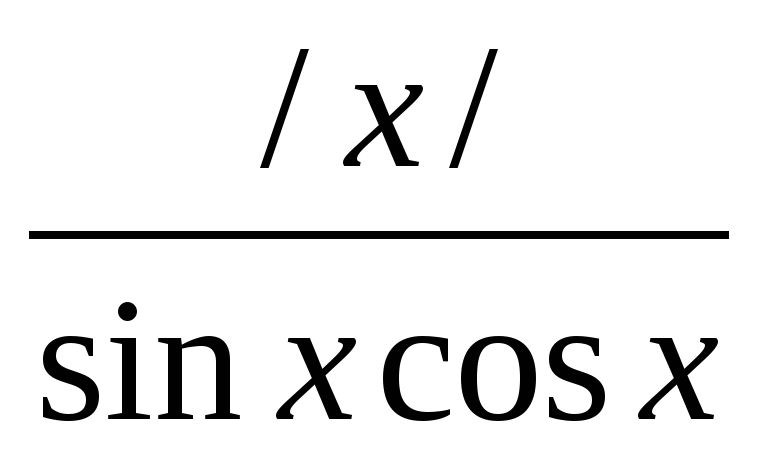

f(-х)= 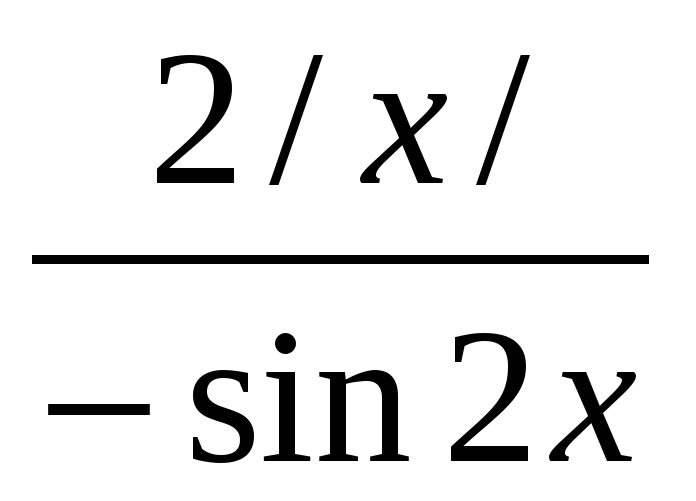=; D(y)=R/πn/2,n€Z;

функция тақ .

Бекіту:

y=sinx y=cosx

Тақ функция D(y)=R Жұп функция

Графигі синусоида косинусоида

[-π/2+2πk; π/2+2πk] ↑ E(y)=[-1;1] [-π+2πk; 2πk] ↑

Т=2π [2πk; π+2πk] ↓

[π/2+2πk; 3π/2+2πk] ↓

Оқушыларды бағалау

Үйге тапсырма беру :

§7, №79 есепті шығарып келу