Тренировочный вариант по математике для 9 класса

ВАРИАНТ 2 Часть 1

Модуль «Алгебра»

№1 Какое из данных ниже чисел является значением выражения .

1. 2) 3) 4)

№2 В таблице приведены размеры штрафов, установленные на территории России с 1 сентября 2013 года, за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации.

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 156 км/ч на участке дороги с максимальной разрешённой скоростью 100 км/ч?

1) 500 рублей 2) 1000 рублей 3) 2000 рублей 4) 5000 рублей

№3 На координатной прямой отмечены числа a, b и c. Какая из разностей a−b, a−c, c−b положительна?

1) a−b 2) a−c 3) c−b 4) ни одна из них

№4 Найдите значение выражения (2⋅10²)⁴​⋅(19⋅10⁻⁶).

№5 При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, на сколько вольт упадёт напряжение с 6-го по 14-й час работы фонарика.

№6 Решите уравнение 4x²=20x.

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

№7 В начале года число абонентов телефонной компании «Запад» составляло 200 тысяч человек, а в конце года их стало 230 тысяч человек. На сколько процентов увеличилось за год число абонентов этой компании?

№8 На диаграммах показано распределение земель по категориям Уральского, Приволжского, Южного и Сибирского федеральных округов. Определите по диаграммам, в каких округах доля земель сельскохозяйственного назначения превышает 50%.

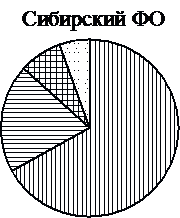
*Прочие земли — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов

1) Уральский ФО 2) Приволжский ФО 3) Южный ФО 4) Сибирский ФО

В ответ запишите номера выбранных вариантов ответов без пробелов, запятых и других дополнительных символов.

№9 Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 21 с машинами и 4 с видами городов. Подарки распределяются случайным образом между 25 детьми, среди которых есть Саша. Найдите вероятность того, что Саше достанется пазл с машиной.

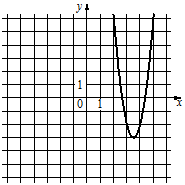
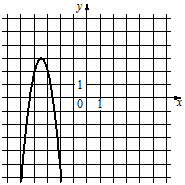
№10 Установите соответствие между функциями и их графиками.

ФУНКЦИИ А) y=−4x²−28x−46 Б) y=4x²−28x+46 В) y=−4x²+28x−46

ГРАФИКИ

1) 2) 3)

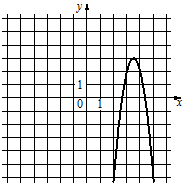
В таблице под каждой буквой укажите соответствующий номер.

№11 Последовательность (b_n) задана условиями: b₁=−6, b_n+1=−2⋅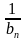 . Найдите b₅.

№12 Найдите значение выражения 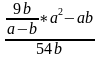при a = - 63, b = 9,6

№13 Мощность постоянного тока (в ваттах) вычисляется по формуле P=I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R, если мощность составляет 283,5 Вт, а сила тока равна 4,5 А. Ответ дайте в омах.

№14 Укажите решение системы неравенств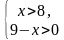

1) 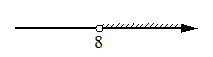2) 3)

4) нет решений

М одуль «Геометрия»

№ 15 Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,2 м, высота большой опоры 2,7 м. Найдите высоту средней опоры. Ответ дайте в метрах.

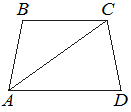
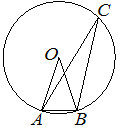№ 16Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 36° и 53° соответственно. Ответ дайте в градусах.

№17 Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 27°. Ответ дайте в градусах.

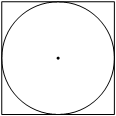
№18 Найдите площадь квадрата, описанного около окружности радиуса 19.

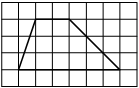
№19 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

№20 Какое из следующих утверждений верно?

1) Диагонали параллелограмма равны.

2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. В ответ запишите номер выбранного утверждения.