
Решение задач по теории вероятности
Щукина Елена Николаевна
МОАУ «СОШ №24» г. Оренбург

Задачи с кубиками и монетами
При решении задач с монетами число всех возможных исходов можно посчитать по формуле п=2 ª , где α – количество бросков
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.
Решение.1:8=0,125 Ответ.0,125
При решении задач с кубиками число всех возможных исходов можно посчитать по формуле п=6 ª , где α – количество бросков
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых. Р
Решение: При бросании кубика 6³= 216 различных исходов, благоприятных 14.14 : 216 = 0,07. Ответ: 0,07.

Задачи на применение признаков делимости
Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Решение: Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел 900:5=180. Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 180:900=0,2. Ответ: 0,2.
В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Решение: Всего в мешке жетонов - 50. Среди них 45 имеют двузначный номер. Таким образом, вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна45 : 50 = 0,9. Ответ:0.9.

Несовместные события. Противоположные события.
Вероятность того, что на тесте по химии учащийся П. верно решит больше 8 задач, равна 0,48. Вероятность того, что П. верно решит больше 7 задач, равна 0,54. Найдите вероятность того, что П. верно решит ровно 8 задач.
Решение: Вероятность решить несколько задач складывается из суммы вероятностей решить каждую из этих задач.
Больше 8: решить 9-ю, 10-ю ...
Больше 7: решить 8-ю, 9-ю, 10-ю ...
Вероятность решить 8-ю =0,54-0,48=0,06. Ответ:0.06

Совместные события Противоположные события.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение: Рассмотрим событие
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52. Ответ: 0, 52.

Независимые события.
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение: Найдем вероятность того, что неисправны оба автомата. Эти события независимые , вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975. Ответ: 0,9975.

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение: Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52. Ответ. 0,52
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решение: В силу независимости событий, вероятность успешно сдать экзамены на лингвистику: 0,6·0,8·0,7 = 0,336, вероятность успешно сдать экзамены на коммерцию: 0,6·0,8·0,5 = 0,24, вероятность успешно сдать экзамены и на «Лингвистику», и на «Коммерцию»: 0,6·0,8·0,7·0,5 = 0,168. Успешная сдача экзаменов на «Лингвистику» и на «Коммерцию» — события совместны е, поэтому вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Тем самым, поступить на одну из этих специальностей абитуриент может с вероятностью 0,336 + 0,24 − 0,168 = 0,408. Ответ: 0,408.
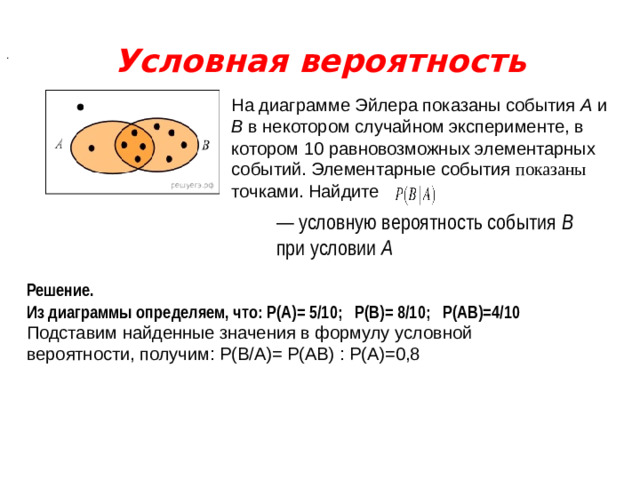
Условная вероятность
.
На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 равновозможных элементарных событий. Элементарные события показаны точками. Найдите
— условную вероятность события B при условии A
Решение.
Из диаграммы определяем, что: Р(А)= 5/10; Р(В)= 8/10; Р(АВ)=4/10
Подставим найденные значения в формулу условной вероятности, получим: Р(В/А)= Р(АВ) : Р(А)=0,8





