Кодирование числовой информации.
Системы счисления
Счет появился, когда человеку потребовалось информировать своих сородичей о количестве обнаруженных им предметов.
Один
или много?
Самым простым инструментом счета были пальцы на руках человека.
С их помощью можно было считать до 5, а если взять две руки, то и до 10.
Одна из таких систем счета впоследствии и стала
общеупотребительной - десятичная.
- Я умею считать до 20!
1 человек - это 20 пальцев, 2 человека - это два раза по 20 пальцев и т.д.
Потребность в записи чисел появилась в очень древние времена, как только люди научились считать. Количество предметов изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине и т.д.
Люди рисовали палочки на стенах или завязывали узелки
Египетская система счисления
Египтяне придумали свою систему счисления около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку
Число 1 245 386 в древнеегипетской записи будет выглядеть
Египетская система счисления
Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки
1
Такими путами египтяне связывали коров
10
Это мерная веревка , которой измеряли земельные участки после разлива Нила.
100
1000
Цветок лотоса
10000
Поднятый палец - будь внимателен!
Головастик
100000
Увидев такое число, обычный человек очень удивится и возденет руки к небу
1000000
Египтяне поклонялись богу Ра , богу Солнца и, наверное, так изображали самое большое свое число
10000000
Алфавитная нумерация
В середине V в. до н. э. появилась запись чисел нового типа, так называемая алфавитная нумерация .
В этой системе записи числа обозначались при помощи букв алфавита.
Славянская кириллическая (непозиционная) нумерация
Чтобы различать буквы и цифры, над числами ставился особый значок — титло ( ~ ).
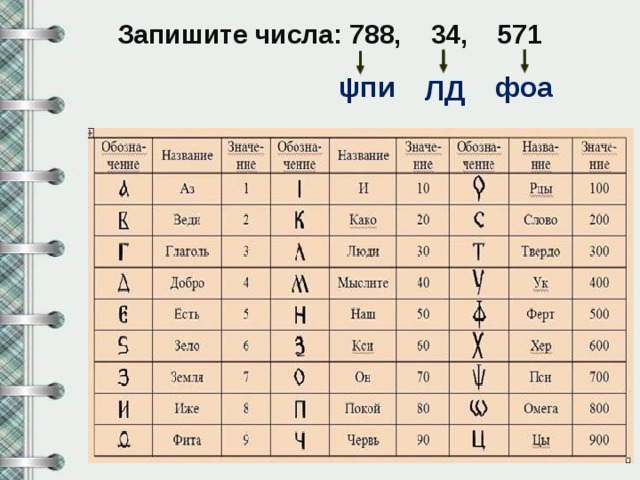
Запишите числа: 788, 34, 571
ψпи
фоа
ЛД
6
Римская система счисления
Возникла в древнем Риме. В ней имеются узловые числа: один, пять и т. д.
Остальные числа получались путем прибавления или вычитания одних узловых чисел из других.
Например, четыре записывается как IV , т. е. пять минус один, восемь - VIII ( пять плюс три), сорок - XL (пятьдесят минус десять), девяносто шесть - XCVI (сто минус десять плюс пять и плюс еще один) и т. д.
Римская система счисления
Правила:
- (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)
- (обычно) не ставят больше трех одинаковых цифр подряд
- если младшая цифра (только одна !) стоит слева от старшей, она вычитается из суммы ( частично непозиционная!)
Примеры:
2389 = M M C C C L X X X I X
6
3999) надо вводить новые знаки-цифры ( V, X , L , C , D , M ) как записать дробные числа? как выполнять арифметические действия: CCCLIX + CLXXIV =? для записи больших чисел (3999) надо вводить новые знаки-цифры ( V, X , L , C , D , M ) как записать дробные числа? как выполнять арифметические действия: CCCLIX + CLXXIV =? Где используется: номера глав в книгах: обозначение веков: « Пираты XX века» циферблат часов номера глав в книгах: обозначение веков: « Пираты XX века» циферблат часов 6" width="640"
Римская система счисления
Недостатки :
- для записи больших чисел (3999) надо вводить новые знаки-цифры ( V, X , L , C , D , M ) как записать дробные числа? как выполнять арифметические действия: CCCLIX + CLXXIV =?
- для записи больших чисел (3999) надо вводить новые знаки-цифры ( V, X , L , C , D , M )
- как записать дробные числа?
- как выполнять арифметические действия: CCCLIX + CLXXIV =?
Где используется:
- номера глав в книгах: обозначение веков: « Пираты XX века» циферблат часов
- номера глав в книгах:
- обозначение веков: « Пираты XX века»
- циферблат часов
6
Запишите римской нумерацией
69
- LXIX
- DXLIII
543
- ZXVI
2016
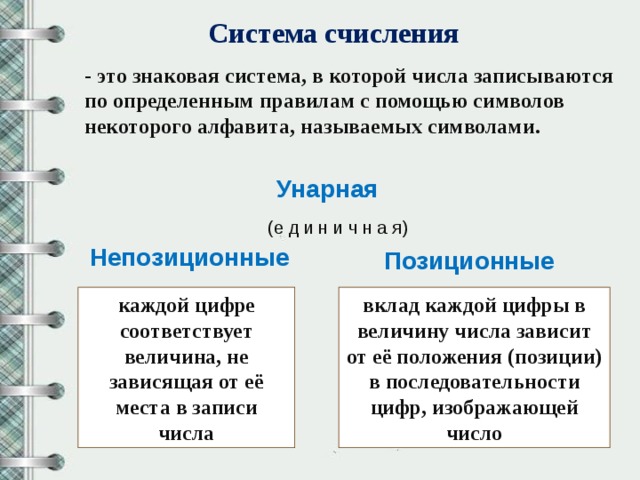
Система счисления
- это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых символами.
Унарная
(е д и н и ч н а я)
Непозиционные
Позиционные
каждой цифре соответствует величина, не зависящая от её места в записи числа
вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число
Позиционные системы счисления
Основание позиционной системы счисления
– это количество различных знаков или символов, используемых для изображения цифр в данной системе счисления.
Алфавит
– набор определенных символов (цифр), используемых в системе счисления
В разные исторические периоды многие народы пользовались разными позиционными системами счисления.
Так, например, двенадцатеричная система (12 часов, «дюжина»); шестидесятиричная (60 минут, 60 секунд).
Десятичная система счисления
Приняв за основание число 10 , получаем знакомую нам десятичную систему счисления:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Всего 10 разных знаков составляют алфавит десятичной системы счисления. Можно записать любое число включая все эти знаки: 237, 12840, 987, 23 ...
Основание системы счисления обозначим буквой q .
Для десятичной системы счисления q =10
Двоичная система счисления
Приняв за основание число 2 , получаем двоичную систему счисления:
0, 1
Всего 2 разных знака составляют алфавит двоичной системы счисления.
Можно записать любое число включая эти знаки: 1, 11, 101 , 110, 10010011 … - обратите внимание: используем только цифры от 0 до 1 .
Для двоичной системы счисления q=2
Позиционные системы счисления
Система счисления
Основание
Двоичная
Алфавит
2
Восьмеричная
8
0, 1
Десятичная
0, 1, 2, 3, 4, 5, 6, 7
10
Шестнадцатеричная
16
0,1,2, 3, 4, 5, 6, 7, 8, 9
0,1,2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F
Разложение чисел по степеням основания
Разряд – это позиция цифры в числе
В записи правый разряд – разряд единиц, затем смещаясь влево - десятки, сотни, тысячи и так далее.
Число 555 в развернутой форме будет выглядеть так :
555 10 = 5 · 10 2 + 5 · 10 1 + 5 · 10 0 ,
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания
555,55 10 = 5 · 10 2 + 5 · 10 1 + 5 · 10 0 + 5 · 10 -1 + 5 · 10 -2
Число в позиционной системе записывается в виде суммы числового ряда степеней основания ( в нашем случае это 10), в качестве коэффициентов которых выступают цифры данного числа.
Разложение чисел по степеням основания
Числа в двоичной системе счисления в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 и 1 :
1111 2 = 1 · 2 3 + 1 · 2 2 + 1 · 2 1 + 1 · 2 0 .
Восьмеричное число может состоять из цифр от 0 до 7, например, 24518 в развернутом виде:
2451 8 = 2 · 8 3 + 4 · 8 2 + 5 · 8 1 + 1 · 8 0
Развернутая запись числа представленного в шестнадцатеричной системе счисления:
А23С 16 = А · 16 3 + 2 · 16 2 + 3 · 16 1 +С · 16 0
Цифра А= 10, С=12.
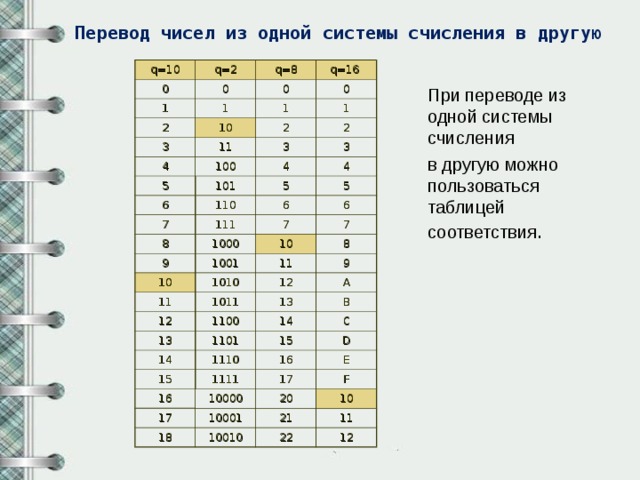
Перевод чисел из одной системы счисления в другую
q=10
q= 2
0
q=8
0
1
q= 16
0
1
2
3
0
1
10
11
4
1
2
2
3
100
5
3
4
6
101
4
7
110
5
5
6
111
8
6
7
1000
9
10
7
10
1001
11
1010
8
11
1011
12
9
12
A
13
13
1100
B
14
1101
14
15
C
15
1110
16
1111
16
D
E
10000
17
17
F
20
10001
18
10
21
10010
11
22
12
При переводе из одной системы счисления
в другую можно пользоваться таблицей соответствия .
Перевод чисел из десятичной системы счисления
Алгоритм перевода целого числа из десятичной системы в систему счисления c другим основанием:
- Последовательно выполнять деление исходного целого числа на основание той системы, в которую переводим, пока частное от деления не окажется равным нулю.
- Записать полученные остатки в обратном порядке, начиная с последнего частного.
Перевод целых десятичных чисел в двоичную систему счисления
Пример 1 . Возьмем десятичное число, например, 11 10 и переведем его в двоичное, выполняя деление на основание 2
Ответ читаем по остаткам - наоборот!
Получили что 11 10 = 1011 2
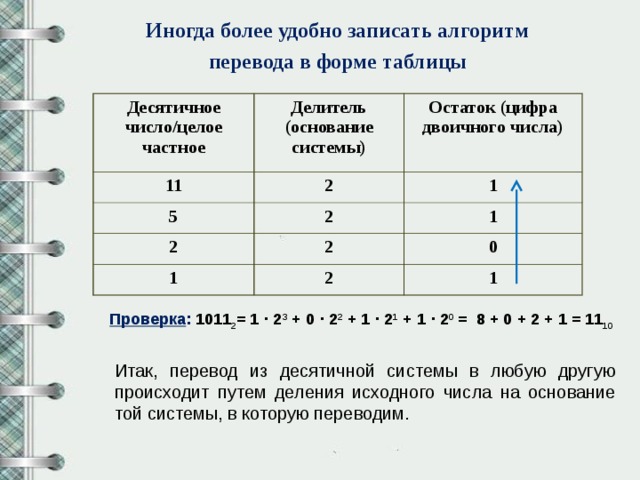
Иногда более удобно записать алгоритм перевода в форме таблицы
Десятичное число/целое частное
Делитель (основание системы)
11
2
5
Остаток (цифра двоичного числа)
1
2
2
1
2
1
0
2
1
Проверка : 1011 2 = 1 · 2 3 + 0 · 2 2 + 1 · 2 1 + 1 · 2 0 = 8 + 0 + 2 + 1 = 11 10
Итак, перевод из десятичной системы в любую другую происходит путем деления исходного числа на основание той системы, в которую переводим.
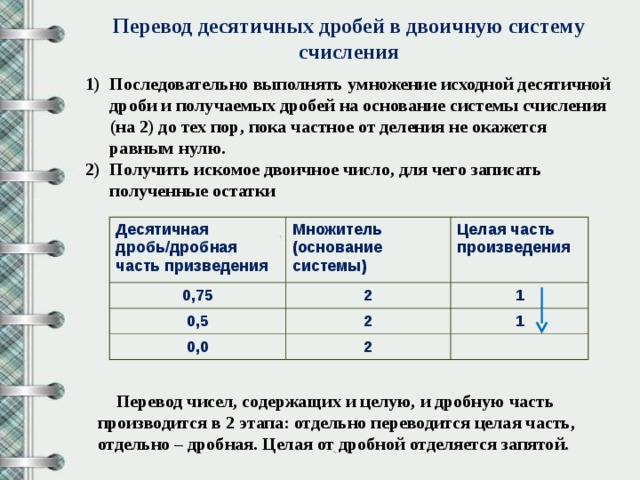
Перевод десятичных дробей в двоичную систему счисления
- Последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы счисления (на 2) до тех пор, пока частное от деления не окажется равным нулю.
- Получить искомое двоичное число, для чего записать полученные остатки
Десятичная дробь/дробная часть призведения
0,75
Множитель (основание системы)
Целая часть произведения
2
0,5
1
0,0
2
1
2
Перевод чисел, содержащих и целую, и дробную часть производится в 2 этапа: отдельно переводится целая часть, отдельно – дробная. Целая от дробной отделяется запятой.
0,
5625
× 2
1
1250
× 2
0
2500
× 2
0
5000
× 2
1
0000
Пример 2 . Перевести десятичную дробь 0,5625 10 в двоичную систему счисления.
Получаем: 0,5625 10 =0,1001 2
Пример 3. Перевести в двоичную систему счисления десятичную дробь 0.7 10 .
0,
1
7
×2
0
4
×2
8
×2
1
1
6
×2
2
Э тот процесс может продолжаться бесконечно . Такой бесконечный процесс обрывают на некотором шаге , когда считают, что получена требуемая точность представления числа.
. . .
Перевод чисел в десятичную систему
счисления
Необходимо записать число в развернутой форме и вычислить его значение в десятичном виде.
Перевод чисел из двоичной системы счисления в десятичную систему счисления
10,11 2 = 1 * 2 1 + 0 * 2 0 + 1 * 2 -1 + 1*2 -2 =1*2 + 0 * 1 + 1* ½ + 1*1/4 = 2,75 10
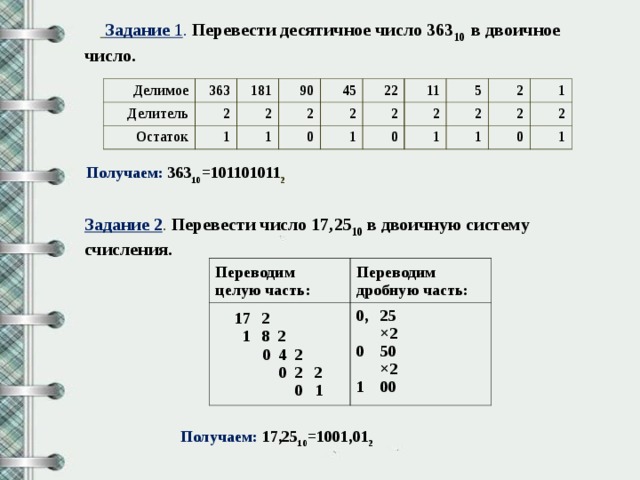
Задание 1 . Перевести десятичное число 363 10 в двоичное число.
Делимое
Делитель
363
2
Остаток
181
90
1
2
2
1
45
22
0
2
11
2
1
2
5
0
1
2
2
1
2
1
2
0
1
Получаем: 363 10 =101101011 2
Задание 2 . Перевести число 17,25 10 в двоичную систему счисления.
Переводим целую часть:
17 2
1 8 2
0 4 2
0 2 2
0 1
Переводим дробную часть:
0, 25
×2
0 50
×2
1 00
Получаем: 17,25 10 =1001,01 2
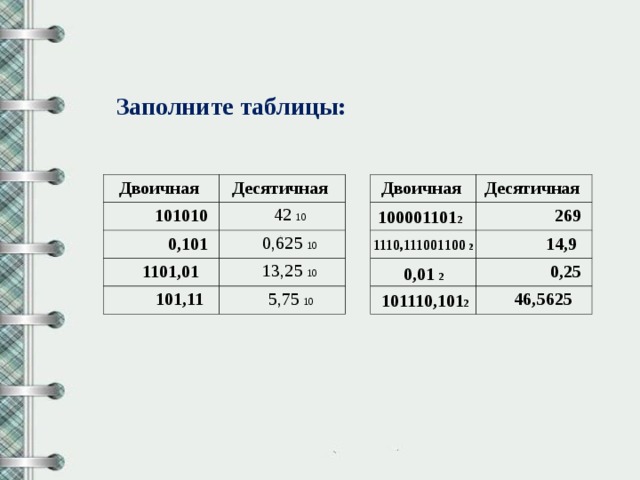
Заполните таблицы:
Двоичная
Двоичная
Десятичная
101010
Десятичная
269
0,101
14,9
1101,01
0,25
101,11
46,5625
42 10
100001101 2
0,625 10
1110,111001100 2
13,25 10
0,01 2
5,75 10
101110,101 2
Проверь себя
1.Что такое система счисления?
2.Чем отличаются позиционные системы счисления от непозиционных, в чем их преимущества?
3. Привести примеры позиционных и непозиционных систем счисления.
4.Что такое основание системы счисления?
5. Как перевести десятичное число в двоичную систему счисления?
6. Как перевести двоичное число в десятичную систему счисления?
