Математический КВН «АССОРТИ»
Цели проведения КВН:
Привитие интереса учащихся к математике;
Развитие математического кругозора, мышления, исследовательских умений учащихся;
Расширение и углубление знаний в области математике;
Развитие способности работать в команде;
Воспитание настойчивости, инициативы.
План проведения КВН:
1. Вступительное слово ведущего.
2. Представление команд.
2. Разминка.
4. Математический калейдоскоп.
5. Конкурс капитанов.
6. Математическая викторина.
7. Конкурс художников.
8. «Черный ящик».
9. Подведение итогов.
Участники:
- команда из учащихся 9 класса;
- команда из учащихся 10 класса;
- жюри (3 педагога, 1 учащийся из 11 класса, 1 учащийся из 12 класса);
- ведущий (учитель математики);
- соведущий (учащийся 10 класса).
Оборудование:
Мультимедиа проектор, ПК, экран, презентация «Математический КВН», «Черный ящик» с предметами (циркуль, часы, шахматы), два чистых плаката с наборами маркеров.
ХОД МЕРОПРИЯТИЯ
Вступительное слово ведущего: (см. слайды 1 и 2)
Привет друзья! Сегодня в школе
Большой и интересный день,
Мы приготовили веселый
Наш школьный вечер КВН.
Все учителя математики часто слышат вопрос: «А зачем мне математика? Мне она в жизни не пригодится».
Слово «математика» пришло к нам из древнего языка: произошло от древнегреческих слов «математикэ» и «матема» - «познание, наука».
Математика – наука о количественных отношениях и пространственных формах действительного мира. И если есть упражнения для развития тела, то математика призвана развивать логическое мышление, внимание,тренировать мозг. Недаром её называют «гимнастикой ума». Математика всегда сопровождала человека в жизни. Она помогала развитию других наук, она развивает у человека такие важные качества личности, как:
логическое мышление;
сильную волю;
устойчивое внимание, сосредоточенность;
хорошую память;
умение логически мыслить: сравнивать, сопоставлять;
способность к творчеству и научной фантазии;
умение прикидывать и оценивать результаты;
работоспособность, интуицию;
находчивость и смекалку.
Я хочу, чтобы вы убедились, что математика – чудесная, не сухая наука и что заниматься ею так же увлекательно, как и играть в КВН.
Итак, мы начинаем КВН!
Разрешите представить членов нашего жюри…
Представление команд (домашнее задание): см.слайд 3
Каждая команда представляет себя, название своей команды, девиз, пожелание соперникам.
Участник 1-ой команды читает:
Ты нам, математика, даешь
Для победы трудностей закалку.
Учится с тобою молодежь
Развивать и волю, и смекалку.
И за то, что в творческом труде
Выручаешь в трудные моменты,
Мы сегодня искренне тебе
Посылаем гром аплодисментов.
Участник 2-ой команды читает:
Почему торжественность вокруг?
Слышите, как быстро смолкла речь?
Явился гость - царица всех наук,
И не забыть нам радость этих встреч.
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Разминка: (см.слайды 4-12)
Задание: проверим вашу смекалку. Кто быстрее разгадает ребус , который сейчас появится на экране. Ваша задача быстрее разгадать ребус, а задача жюри следить за тем кто быстрее даст правильный ответ, тому и засчитать балл за ответ.
И так будьте внимательны: первый ребус - слайд №5, правильный ответ – аксиома; второй ребус - слайд №7, правильный ответ – апофема; третий ребус – слайд №9, правильный ответ – вектор; четвертый ребус - слайд №11, правильный ответ – конус.
Жюри подводит итоги.
Математический калейдоскоп: (см.слайды 13-24)
Предлагаю вашему вниманию ознакомится с основоположниками математики, о многих из которых вы уже слышали, но может не всегда знали какие великие открытия они совершили.
Презентация «Творцы математики и их открытия»
Фалес Милетский (625 до н.э. - 548 до н.э.)
Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и, вообще, первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России.
Фалесу Милетскому приписывают простой способ определения высоты пирамиды. В солнечный день он поставил свой посох там, где оканчивалась тень от пирамиды. Затем он показал, что как длина одной тени относится к длине другой тени, так и высота пирамиды относится к высоте посоха.
Теорема Фалеса — одна из теорем планиметрии. Формулировка теоремы:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Пифагор (греч. Πυθαγόρας ο Σάμιος) ( 580 г. и умер ок. 500 г. до н.э.)
Историю его жизни трудно отделить от легенд, представляющих Пифагора в качестве полубога и чудотворца, совершенного мудреца и "великого посвященного" во все тайные доктрины греков и варваров. По преданию, Пифагор объездил весь свет и собрал свою философию из различных систем, к которым имел доступ.
Теорема Пифагора Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Евклид древнегреческий математик (365-300 до. н. э.)
Как-то царь Птолемей I спросил Евклида, нет ли более короткого пути для изучения геометрии, чем штудирование "Начал". На это Евклид смело ответил, что "в геометрии нет царской дороги".
Евклид является для нас автором "Начал", по которым учились математики всего мира.Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. "Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве.
Архимед из Сиракуз (287 г. до н.э. – 212 г. до н.э.)
Архимед родился в 287 году до нашей эры в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали самую большую в мире библиотеку.
Великие открытия Архимеда
АРХИМЕДА ЗАКОН: на всякое тело , погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Закон Архимеда справедлив и для газов.
АРХИМЕДОВ ВИНТ - водоподъемная машина, вал с винтовой поверхностью, установленный в наклонной трубе, нижний конец которой погружен в воду. При вращении (напр., от ветряного или другого двигателя) винтовая поверхность вала перемещает воду по трубе на высоте до 4 м.
АРХИМЕДОВА СПИРАЛЬ - плоская кривая, описываемая точкой M, равномерно движущейся по прямой OA, в то время как эта прямая равномерно вращается в плоскости вокруг одной из своих точек O. Уравнение в полярных координатах r=af, где a - постоянная.
Эратосфен Киренский (Eratosthenes, Ερατοσθδνη) (ок. 275-194 до н.э.)
Один из самых разносторонних ученых античности. Особенно прославили Эратосфена труды по астрономии, географии и математике, однако он успешно трудился и в области филологии, поэзии, музыки и философии, за что современники дали ему прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. "второй", по-видимому, также не содержит ничего уничижительного: им желали показать, что во всех науках Эратосфен достигает не высшего, но превосходного результата.
Решето Эратосфена: самым знаменитым математическим открытием Эратосфена стало т.н. "решето Эратосфена", с помощью которого находятся простые числа.
Конкурс капитанов (см.слайд 25-29)
А теперь конкурс капитанов. В начале хочу познакомить вас с понятием математического софизма.
СОФИЗМ – (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.
Каждому капитану предлагается по сафизму и через две минуты они должны ответить на вопрос, где же допущена ошибка?
1 софизм: “Два умножить на два будет пять”
2*2=4
4 /4=5 /5,
вынесем за скобки слева 4, справа5
4(1 /1)=5(1 /1),
разделим левую и правую часть на (1/ 1), получим
4=5, откуда следует
2*2=5.
2 софизм: «Один рубль не равен 100 копеек»
1 р=100 коп
10 р=1000 коп
Умножим обе части этих верных равенств, получим:
10 р=100000 коп, откуда следует:
1 р=10000 коп.
Жюри подводит итоги конкурса капитанов.
Математическая викторина (см.слайды 30-31)
Предлагаю вашему вниманию задания и вопросы на смекалку. Та команда которая быстрее даст правильный ответ та и получает балл. В конкурсе побеждает та команда которая наберет больше всех баллов.
Задания для викторины
1.Летела стая уток. Одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько летело уток? ( 3 )
2. Хорошо известно, что 5²= 25, 10²= 100, половина в квадрате -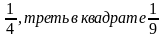
. А чему равен угол в квадрате? ( 90̊ )
3. Число 666 требуется увеличить в 1,5 раза, не производя никаких арифметические действий над ними. Как это сделать? ( 999 )
4.Сколько граней имеет неочищенный шестигранный карандаш? (8 граней)
5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков? (за 6 дней)
6.Какое число делится на все числа без остатка ? ( 0 )
7.Половина числа 12 оказалось, равной 7. Как это могло случиться? (ХII)
8.Что тяжелее: килограмм десятикопеечных может или полкилограмма двадцатикопеечных? ( 1кг ˃0,5 кг металла )
9.Какой русский писатель окончил физико-математический факультет?
( Грибоедов )
10. Летела стая уток, всего 5. Одну убили, сколько осталось? ( 1 )
11.На озере росли лилии. Каждый день их число удваивалось, и на 20-ый день заросло всё озеро. На какой день заросла половина озера?
( на 19 день )
12.Часы с боем отбивают один удар за 1 секунду. Сколько времени потребуется часам, чтобы отбили 12 часов? ( 11 секунд )
13.Её знакомство с математикой произошло в 8 лет, т.к. стены её комнаты были оклеены листами с записями лекций по математике профессора Островского. Кто она? ( Ковалевская )
14.В каком случае верно равенство? 19+15=10 ( 7ч+3ч=10ч )
15. Как из числа 1888 получить 1?
16. Есть 2 сковородки. На каждой помещается один блин. Надо пожарить три блина с двух сторон. Каждая сторона блина жарится 1 минута. За какое наименьшее время это можно сделать? (3 минуты)
17.Напишите, использовав 3 цифры, наибольшее возможное число ( 9 )
18.Из 4 спичек сложено число VII. Как можно переложить две спички, чтобы получилось число 5? число 1? ( 5=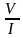 
1= 
1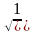9. Двое пойдут - 5 грибов найдут. Четверо пойдут – много ли найдут?
2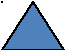
0. Требуется провести прямую линию так, чтобы она пересекала все стороны треугольника. Как это сделать?
Жюри подводит итоги викторины.
Конкурс художников (см.слайды 32-33)
Задание для команд: нарисовать фигуру человека или животного
только с помощью геометрических фигур. Побеждает та команда, которая изобразит фигуру, наиболее правдиво и при этом использует наибольшее количество геометрических фигур.
Жюри оценивает рисунки команд и определяет победителя в конкурсе.
«Черный ящик» (см.слайд 34)
Отгадайте, что лежит в «Черном ящике»:
Вносят ящик с циркулем. Вопросы подсказки:
Один из аналогов этого предмета пролежал в земле 2000 лет. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В нашей стране это было впервые обнаружено в Нижнем Новгороде. За многие годы конструкция этого предмета практически не изменилась, настолько была совершенна. В Древней Греции умение пользоваться этим предметом считалось верхом совершенства, а умение решать задачи с его помощью – признаком большого ума. Этот предмет незаменим в архитектуре и строительстве для выполнения чертежей.
Вносят ящик с шахматами. Вопросы подсказки:
Историк 20 века Роуз сказал: «Это задушевная беседа без слов, лихорадочная активность, триумф и трагедия, надежда и отчаяние, жизнь и смерть, поэзия и наука, древний Восток и современная Европа». Родина –Индия. Возраст-15 столетий. Имя изобретателя неизвестно. Старинное название – чатуранга. Когда в каждой семье можно будет найти эту игру, появится надежда на то, что со временем исчезнет скудность истинных государственных умов. Это дворцовая жизнь в миниатюре. В этой игре есть кони и слоны.
Вносят ящик с часами. Вопросы подсказки:
История изобретения этого предмета история насчитывает тысячи лет. Эта вещь на протяжении веков постоянно совершенствовалась и претерпевала изменения, уменьшалась в своих размерах. Слово, которым эта вещь называется, не имеет единственного числа. В математике без этой вещи трудно обойтись. Особенно при решении задач на движение. Почти у каждого из нас есть эта замечательная вещь: механическая, электронная, противоударная, водонепроницаемая.
Подведение итогов КВН: (см.слайд 35)
Вот и подходит к концу наша сегодняшняя встреча, жюри подводит последние итоги, объявите их пожалуйста. Слово жюри.
В заключении хочу прочитать стихи, посвященные математики:
О, математика, земная!
Гордись, прекрасная собой.
Ты всем наукам – мать родная
И дорожат они тобой!
Строга, логична, величава,
Стройна в пролете, как стрела,
Твоя не меркнувшая слава
В веках бессмертье обрела.
Я славлю разум человека,
Дела его волшебных рук,
Надежду нынешнего века,
Царицу всех земных наук!
Спасибо за внимание!!!
