Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 10 г. Апатиты
КОНСПЕКТ
интегрированного урока информатика-математика
в 11 классе
«Приближённое решение уравнений вида f1(x)= f2(x)
c помощью электронных таблиц»
|
| Автор: Фадеева Марина Николаевна, учитель информатики высшей категории |
Апатиты
2012
|
| Хороших методов существует столько, сколько существует хороших учителей. Д. Пойа.
|
Цели:
Образовательные:
Научить графическому методу нахождения корней уравнений вида f(x)=0 грубо приближённо с применением электронных таблиц;
Научить искать решение с заданной точностью методом Подбора параметра с помощью надстроек в электронных таблицах.
Развивающие:
Установление межпредметных связей;
Показать применение компьютера (электронных таблиц) во многих областях практической и научной деятельности и в частности – математике;
Развивать у учащихся умения анализировать задачу перед выбором способа её решения.
Воспитательные:
Установление взаимных контактов и обмен опытом между учащимися и преподавателем;
Предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах.
Методы:
информационный (словесный);
наглядно-иллюстративный;
практический.
информационно-коммуникационный;
проблемного обучения.
Тип урока: интегрированный
Оборудование: персональные компьютеры, мультимедийный проектор, локальная компьютерная сеть.
Дидактические средства: компьютерная презентация «Графический метод-математика», книга MS Excel.
Прикладные программы: Редактор презентаций MS PowerPoint, табличный процессор MS Excel
План и хронометраж урока
| № п/п | Вид работы | Время |
| 1 | Организационный момент. | 2 мин |
| 2 | Самоопределение к деятельности | 4 мин |
| 3 | Постановка учебной задачи | 9 мин |
| 4 | Открытие и включение в систему знаний нового понятия | 10 мин |
| 5 | Динамическая пауза. | 1 мин |
| 6 | Этап первичного закрепления знаний | 15 мин |
| 7 | Подведение итогов | 3 мин |
| 8 | Постановка домашнего задания | 1 мин |
| ИТОГО | 45 мин |
Ход проведения
Организационный момент
Приветствие. Проверка наличия обучающихся. Подготовка к работе.
Самоопределение к деятельности
Прежде чем мы будем изучать новую тему, давайте вспомним, какие задачи мы с вами решали с помощью электронных таблиц (ЭТ) и в каких областях человеческой деятельности их можно использовать.
На экране – Лист 2 – «Расход эн.» демонстрируется задание, которое мы выполняли в 9 классе: рассчитать расход электроэнергии и сумму оплаты при наличии электроплиты.
Вопрос к классу: Где можно использовать электронные таблицы?
Ответ: ЭТ можно использовать в работе бухгалтерии жилищно-коммунального хозяйства.
На экране Лист 3 – «Библ.» – демонстрируется задание, которое мы выполняли в 10 классе – библиотека. Зная количество выданных книг по разным предметам, мы вычисляли сколько книг получил каждый класс, сколько должно быть книг получено, сколько необходимо заказать и наглядно увидели на диаграмме какие классы нуждаются в учебниках.
Вопрос к классу: Где можно использовать электронные таблицы?
Ответ: ЭТ можно использовать в работе школьной библиотеки.
На экране Лист 4 – «Зарплата» – демонстрируется задание, которое мы выполняли в 10 классе – Расчёт заработной платы. С помощью вспомогательной таблицы, находящейся на другом листе, мы вставляли в главную таблицу оплату за день в зависимости от разряда. Затем вводили количество отработанных дней и рассчитывали заработную плату сотрудникам.
Вопрос к классу: Где можно использовать электронные таблицы?
Ответ: ЭТ можно использовать в работе бухгалтерии.
На экране Лист 5 «Итог. отчёт» – демонстрируется задание, которое мы выполняли в 11 классе – Составление итоговых отчётов. Имея таблицу закупок разного типа товара, средствами MS Excel мы составили итоговый отчёт, который сгруппировал технику по типам.
Вопрос к классу: Где можно использовать электронные таблицы?
Ответ: ЭТ можно использовать в работе любой организации для составления отчётов по закупкам.
На экране Лист 6 – «Сводн. табл.» – демонстрируется задание, которое мы выполняли в 11 классе. Мы научились создавать сводные таблицы, с помощью которых можно одновременно подвести итоги, отсортировать данные и произвести фильтрацию. К тому же одни и те же данные можно представлять в разных формах.
На экране Листы 7-10 – «Конс. отч.1», «Конс. отч.2», «Конс. отч.3», «Конс. отч.4», – демонстрируются задания из 11го класса. Мы научились создавать консолидированные отчёты, когда данные находятся на разных листах рабочей книги, а средствами MS Excel мы смогли отобразить их в общей итоговой таблице.
Вопрос к классу: Где можно использовать электронные таблицы?
Ответ: ЭТ можно использовать в работе магазина по продаже компьютерной техники.
Постановка учебной задачи
Сегодня на уроке мы увидим, как можно использовать ЭТ на уроках математики при изучении темы «Приближённое решение уравнений вида f1(x)= f2(x)».
На экране Лист 1– «Тема». Записываем тему урока: «Приближённое решение уравнений вида f1(x)= f2(x) c помощью электронных таблиц»
На экране Лист 11 – «Задача». Формулируется задача, которую предстоит решить сегодня на уроке: Найти приближённое (графическое) решение уравнения x3/10=sin x на интервале от -2,5 до 2,5 с шагом 0,5.
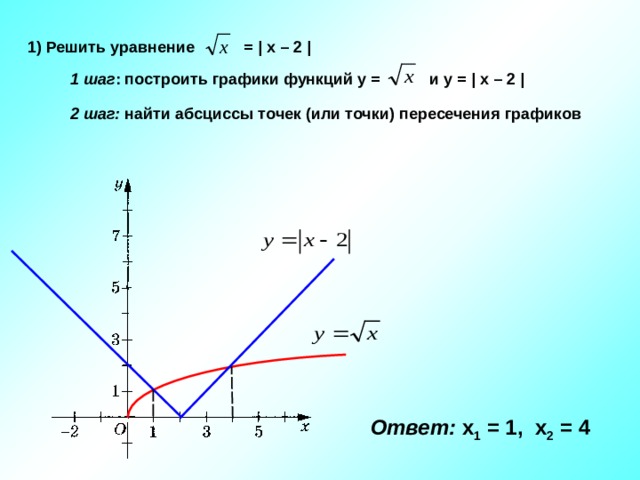
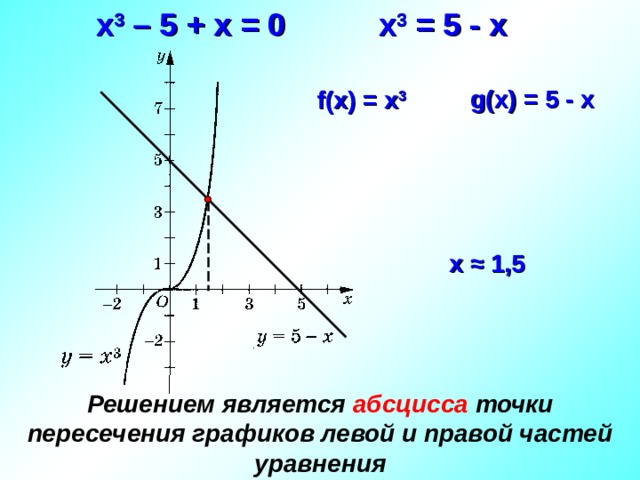
Прежде давайте посмотрим как вы решаете подобную задачу на уроке математики. Демонстрируются 1, 2 и 3 слайды презентации «Графический метод нахождения корней уравнений».
Теперь давайте посмотрим как эту задачу намного быстрее можно решить с помощью ЭТ.
На экране Лист 12 – «Графики». Создайте новую книгу и на 1 листе заполните таблицу значений функций: y1=sin(x) и y2=x3/10 на интервале [-2,5;2,5] с шагом 0,5. Протабулируйте обе функции на этом интервале.
Затем постройте графики функций. Не забудьте отформатировать ось ОХ, т.к. Excel проставляет не точки отрезка ОХ, а их номера. Координаты точек пересечения графиков и будут корнями уравнения: х1 -2 х2 0 х3 2.
Открытие и включение в систему знаний нового понятия
Если требуется найти решение с заданной точностью, то можно использовать метод подбора параметра.
Формулируется задача 2 (под графиками): С использованием компьютерной модели в электронных таблицах с точностью до 4х знаков методом подбора параметра решить уравнение х3/10-sin x = 0.
На экране Лист 14 – «Подбор пар.» – Объяснение метода по шагам.
1. Скопируем значения х с 1го листа и протабулируем функцию х3/10-sin x на том же промежутке и с тем же шагом.
2. Установим точность представления чисел в ячейках с точностью до 4х знаков.
3. Построим график функции. По нему грубо приближённо можно определить, что уравнение имеет корни: х1 -2 х2 0 х3 2.
4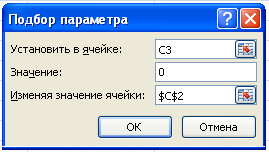
. Выделим ячейку, содержащую значение функции, наиболее близкую к нулю, например, С3 и введём команду: Данные – Анализ «что-если» – Подбор параметра.
5. Выпадет окно: «Подбор параметра»
В поле «Значение» введём требуемое значение функции (в данном случае – 0).
В поле «Изменяя значение ячейка» введём адрес ячейки С2 (Щёлкнем по ячейке С2), в которую будет производиться подбор значений аргумента.
6. На панели «Результат подбора параметра» будет выведена информация о величине подбираемого и подобранного значения.
7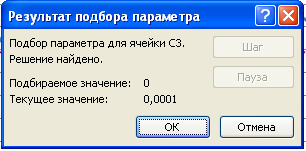
. В ячейке С2 появится подобранное значение: -2, 0648.
8. Повторяем подбор параметра для ячейки значения функции К3. В ячейке аргумента К2 появится подобранное значение: 2,0648.
Таким образом, корни уравнения с точностью до 4х знаков после запятой найдены: х1 -2, 0648 х2 0,0000 х3 2,0648
Динамическая пауза
Этап первичного закрепления знаний
Выдаются задания на два варианта для самостоятельной и домашней работы. Нужно выполнить только первый номер, остальные – дома. Необходимо вначале построить графики функций с помощью ЭТ и найти корни грубо приближённо. Затем уточнить корни методом Подбор параметра. Ответы записать в выданные таблицы. Сохранить задание и переслать по сети на диск students. Первые из переславших работы (1 вар и 2 вар) будут демонстрировать их всему классу на экране проектора.
| Задания для самостоятельной и домашней работы 1 вар |
| Найти приближённое (графическое) решение (решения) уравнений и методом Подбора параметра уточнить корень (корни) с точностью до 4х знаков после запятой:
x3 = cos x на интервале от –2,5 до 2,5 с шагом 0,5 x2 = sin x - 0,1 на интервале от –1,5 до 1,5 с шагом 0,5 1 3  x3=sin x на интервале от –2 до 2 c шагом 0,5
Записать ответы в таблицу: | уравнение | корень (корни) грубо приближённо | уточнённый корень (корни) методом Подбора параметра | |
x3 = cos x |
|
| | x2 = sin x - 0,1
|
|
| | 1 3 x3=sin x
|
|
|
|
| Задания для самостоятельной и домашней работы 2 вар
|
| Найти приближённое (графическое) решение (решения) уравнений и методом Подбора параметра уточнить корень (корни) с точностью до 4х знаков после запятой: x2 = соs x на интервале от –2,5 до 2,5 с шагом 0,5 x3 = sin x + 0,5 на интервале от –1,5 до 1,5 с шагом 0,5 1 x2 = sin x на интервале от –1,5 до 2 с шагом 0,5 2 Записать ответы в таблицу: | уравнение | корень (корни) грубо приближённо | уточнённый корень (корни) методом Подбора параметра | |
x2 = соs x |
|
| |
x3 = sin x + 0,5 |
|
| | 1 2 x2 = sin x
|
|
|
|
Обучающиеся выполняют работу, а учитель ожидает ответы на сетевом диске students. По мере поступления заданий учитель их проверяет и приглашает к экрану проектора первого из обучающихся, приславшего верное решение из 1го варианта, затем 2го. Ребята демонстрируют свои работы, проговаривая всю последовательность действий, остальные – сверяют с правильными:
Ответы к 1 варианту
| уравнение | корень (корни) грубо приближённо | уточнённый корень (корни)
методом Подбора параметра |
| |
x3 = cos x
|
x=0,8
|
x=0,8654
| |
x2 = sin x - 0,1 | x1=0,1 x2=0,7 | x1=0,1130 x2=0,7740 | |
1 x3=sin x 3 | x1=-1,4 x2=0 x3=1,4 | x1=-1,4381 x2=0,0000 x3=1,4381 |
|
|
|
Ответы ко 2 варианту | уравнение | корень (корни) грубо приближённо | уточнённый корень (корни)
методом Подбора параметра | | x2 = соs x | x1=-1 x2=1 | x1=-0,8243 x2=0,8243 | | x3 = sin x + 0,5
| x=1,2 | x=1,1185 | | 1 x2 = sin x 2 | x1=0 x2=1,4 | x1=0,0000 x2=1,4047 |
|
|
Подведение итогов
На экране Лист 15 – «Схема» – подведение итогов урока: в каких случаях необходимо использовать графический метод и метод подбора параметра.
Постановка домашнего задания
Т.к. задание объёмное, ребята успевают выполнить только задание № 1. Поэтому, остальные задания они выполнят дома и отметка будет выставлена на следующем уроке.
. Выделим ячейку, содержащую значение функции, наиболее близкую к нулю, например, С3 и введём команду: Данные – Анализ «что-если» – Подбор параметра.
. В ячейке С2 появится подобранное значение: -2, 0648.
