Физические основы механики

• Векторным произведением вектора на вектор назовем вектор , модуль которого

а) вектор ортогонален векторам и ;

б) из конца вектора кратчайший поворот от вектора (первого сомножителя) к вектору (второму сомножителю) виден против часовой стрелки. (Начала векторов предполагаются совмещенными).          

• Производная. Если f(x) - непрерывная функция одной переменной, то ее производной называется

Пример:

• Пример:
• Пример:
• Пример:
• Пример:

• Частная производная . f ( x, y, z ) - непрерывная функция нескольких переменных. Частной производной по одной из переменных называется:
• Полная производная сложной функции f(x, y, z, t ), где x = x(t), y = y(t), z = z(t),

t – параметр (время).

Функция

Производная

0

• Неопределенный интеграл

0

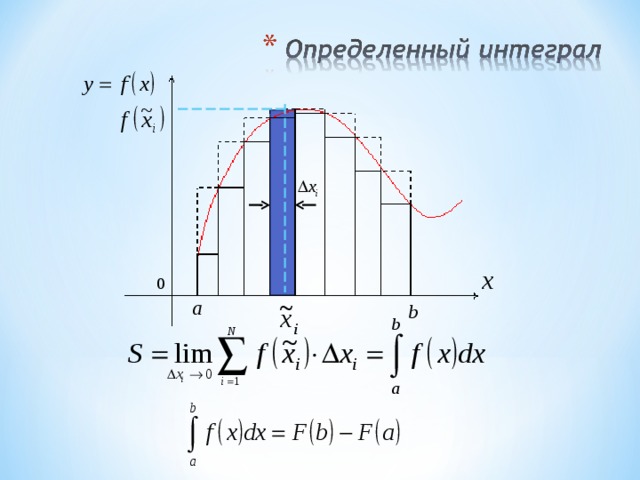
Понятие определенного интеграла введем на примере вычисления площади криволинейной трапеции, т.е. фигуры ограниченной графиком функции y=f(x), осью x и прямыми, перпендикулярными оси и проходящими через точки а, b. Разобьем отрезок на бесконечно малые элементы длиной  xi и обозначим некоторое среднее значение координаты i-го элемента. На каждом элементе построим прямоугольник высотой f(xi), площадь которого  Si=f(xi)  xi. Вычисление производится по формуле Ньютона –Лейбница, где F(x) – первообразная f(x) на отрезке.

§1. Пространство, время. Системы отсчета

Пространство и время - формы существования материи, органически связанные между собой :

наблюдаемый мир четырехмерен .

Пространство - порядок существования материальных объектов. Время - порядок смены явлений.

Положение любого движущегося тела определяется по отношению к телу отсчета, поэтому механическое движение относительно .

Тело отсчета Произвольно выбранное тело, относительно которого определяется положение других (движущихся) тел.

Система отсчета – это совокупность

тела отсчета , связанной с ним

системы координат и часов .

Пространство и время не существуют отдельно от материи. Пространство выражает порядок существования материальных объектов. Время отражает порядок смены явлений. Не существует явлений, которые протекали бы вне пространства и времени. Пространство и время, как формы существования материи, органически связаны между собой: наблюдаемый мир четырехмерен.

Три измерения пространственные, одно измерение связано со временем.

Механическое движение имеет строго определенное содержание только при указании, относительно каких тел перемещается рассматриваемый объект. В этом и заключается фундаментальное свойство природы – всякое движение относительно. Поэтому для описания механического движения необходимо ввести систему отсчета. Система отсчета включает тело отсчета для фиксации положения рассматриваемого объекта и эталонный процесс для фиксации времени. С помощью часов отмечаются моменты времени, соответствующие мгновенным положениям движущегося тела. Совокупность тела отсчета, системы координат и часов называется системой отсчета .

Примером простейшей системы координат служит прямоугольная декартова система координат. Она реализуется тремя взаимно перпендикулярными плоскостями, жестко связанными с телом отсчета. Точка их пересечения называется началом координат, а линии их пересечения – координатными осями. Координатами точки служат три расстояния от нее до координатных плоскостей, обычно обозначаемые x, y, z. Соответствующие координатные оси обозначаются ox, oy, oz. Чаще всего используется правовинтовая система: если в такой системе посмотреть с конца орта I на оси ox, oy, то кратчайший поворот от оси x к оси y будет происходить против часовой стрелки.

9

где i, j, k – единичные векторы (орты).

Число независимых координат, однозначно определяющих положение тела (или системы тел) в пространстве, называется числом степеней свободы тела (или системы тел).

Любые k величин q 1 , q 2 , …, q k , однозначно определяющие положение системы, называются обобщенными координатами .

Это соответствует связям между ортами координатной системы: .

В кинематике число принципиально равноценных систем координат бесконечно. Стремятся использовать такую систему, которая максимально облегчает решение рассматриваемой задачи. Кроме декартовой, наиболее часто используются цилиндрическая и сферическая системы. Число независимых координат, однозначно определяющих положение тела (или системы тел) в пространстве, называется числом степеней свободы тела (или системы тел).

В общем случае число степеней свободы системы не совпадает с общим числом пространственных координат. Более того, величины, о которых идет речь в определении числа степеней свободы, не обязательно должны иметь смысл пространственных координат, поскольку в зависимости от условий задачи может оказаться более удобным выбор каких-либо других координат. Любые k величин q1, q2, …, qk, однозначно определяющие положение системы, называют ее обобщенными координатами.

9

• Свободная материальная точка :

число степеней свободы k = 3 ;

• N-точек : k = 3N .
• Точка не свободна, а движется по поверхности сферы радиуса R с центром в начале координат

Три координаты x, y, z связаны между собой соотношением

т.е. k = 3 – n = 3 – 1 = 2 , где n – число связей.

Обобщенные координаты: q 1 = x, q 2 = y или q 1 =  , q 2 =  .

• Точка движется по заданной кривой например , точка движется по окружности R в плоскости oxy, (две связи n=2):

- уравнение сферы и z = 0 – уравнение плоскости

k = 3 – n = 3 – 2 = 1 .

Обобщенные координаты q = x или q =  .

В общем случае число степеней свободы тела или системы тел, и, следовательно, обобщенных координат k = 3N - n , где N – число материальных точек входящих в состав тела.

У одной свободной материальной точки число обобщенных (как и декартовых) координат равно трем, т.е. число степеней свободы в этом случае k=3; у N-точек k=3N.

Если точка не свободна, а движется, например, по поверхности сферы заданного радиуса R с центром в начале координат, то три координаты x, y, z связаны между собой соотношением R= (x 2 +y 2 +z 2 ) ½ . Иными словами имеются только две независимые координаты. Задавая их можно из приведенного выражения найти третью. В этом случае говорят, что на систему «материальная точка» наложена жесткая связь. Следовательно, при наличии жестких связей между точками число степеней свободы уменьшается на единицу и становится равным k=3-n=3-1=2, где n – число связей, т.е. Достаточно ввести две координаты, например x, y или   , и положение точки будет задано однозначно. В этом случае обобщенными координатами будут q1=x, q2=y или q1=  , q2=  .

Если точка может двигаться вдоль заданной кривой, то число степеней свободы уменьшается до одной, так как число связей увеличивается до n=2: k=3-n=3-2=1. Например, точка может перемещаться по сфере радиусом R, оставаясь в плоскости oxy, т.е. По окружности с радиусом R, лежащей в плоскости oxy. В этом случае на координаты точки x, y, z наложены две связи: Так для задания положения необходимо задать: R= (x 2 +y 2 +z 2 ) ½ -уравнение сферы и z=0 – уравнение плоскости. В качестве обобщенной координаты можно выбрать q=x или q=  .

В общем случае число степеней свободы тела или системы тел и, следовательно обобщенных координат k=3N-n, где N – число материальных точек входящих в состав тела или системы тел.

Число степеней свободы «жесткого» треугольника с вершинами А(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3), k=3N-n = 6, где n =3 – число связей наложенных на координаты x1, y1, z1, x2, y2, z2, x3, y3, z3. Уравнения связей имеют следующий вид:

Здесь l12,l32, l13 – длины трех сторон рассматриваемого треугольника.

«Жесткий»треугольник моделирует абсолютно твердое тело, поэтому у произвольного свободного твердого тела число степеней свободы также будет равно 6, из которых 3 описывают поступательное, а 3 – вращательное движения тела. Для определения положения твердого тела необходимо задать:

• Три координаты, фиксирующие положение какой-то точки этого тела в пространстве;
• Два угла для определения направления оси, проходящей через выделенную точку тела;
• Угол поворота тела относительно этой оси.

Таким образом для абсолютно твердого тела число степеней свободы равняется шести. Для каждой степени свободы системы должно быть записано свое уравнение движения, т.е. количество скалярных уравнений движения системы должно совпадать с ее числом степеней свободы.

Итак, для описания механического движения тела (системы тел) необходимо прежде всего задать систему отсчета. Описать механическое движение тела – это означает, что нужно описать механическое движение всех отдельных малых частей этого тела (материальных точек).

9

• «Жесткий» треугольник А( x 1 , y 1 , z 1 ), B (x 2 , y 2 , z 2 ), C(x 3 , y 3 , z 3 ):

k = 3N - n = 6 ,

где n =3 – число связей на координаты. Уравнения связей:

Моделирует абсолютно твердое тело, у которого тоже будет 6 степеней свободы. Из них 3 описывают поступательное движение, 3 – вращательное.

• Для определения положения необходимо задать:

• x, y, z; 2)  ,  ;  .

Если тело закреплено в точке (еще три дополнительные связи), то тело может лишь вращаться вокруг этой точки, остается только три степени свободы.

У твердого тела, которое может вращаться вокруг закрепленной оси, остается одна степень свободы, характеризуемая одной обобщенной координатой – углом поворота вокруг этой оси.

У одной свободной материальной точки число обобщенных (как и декартовых) координат равно трем, т.е. число степеней свободы в этом случае k=3; у N-точек k=3N.

Если точка не свободна, а движется, например, по поверхности сферы заданного радиуса R с центром в начале координат, то три координаты x, y, z связаны между собой соотношением R= (x 2 +y 2 +z 2 ) ½ . Иными словами имеются только две независимые координаты. Задавая их можно из приведенного выражения найти третью. В этом случае говорят, что на систему «материальная точка» наложена жесткая связь. Следовательно, при наличии жестких связей между точками число степеней свободы уменьшается на единицу и становится равным k=3-n=3-1=2, где n – число связей, т.е. Достаточно ввести две координаты, например x, y или   , и положение точки будет задано однозначно. В этом случае обобщенными координатами будут q1=x, q2=y или q1=  , q2=  .

Если точка может двигаться вдоль заданной кривой, то число степеней свободы уменьшается до одной, так как число связей увеличивается до n=2: k=3-n=3-2=1. Например, точка может перемещаться по сфере радиусом R, оставаясь в плоскости oxy, т.е. По окружности с радиусом R, лежащей в плоскости oxy. В этом случае на координаты точки x, y, z наложены две связи: Так для задания положения необходимо задать: R= (x 2 +y 2 +z 2 ) ½ -уравнение сферы и z=0 – уравнение плоскости. В качестве обобщенной координаты можно выбрать q=x или q=  .

В общем случае число степеней свободы тела или системы тел и, следовательно обобщенных координат k=3N-n, где N – число материальных точек входящих в состав тела или системы тел.

Число степеней свободы «жесткого» треугольника с вершинами А(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3), k=3N-n = 6, где n =3 – число связей наложенных на координаты x1, y1, z1, x2, y2, z2, x3, y3, z3. Уравнения связей имеют следующий вид:

Здесь l12,l32, l13 – длины трех сторон рассматриваемого треугольника.

«Жесткий»треугольник моделирует абсолютно твердое тело, поэтому у произвольного свободного твердого тела число степеней свободы также будет равно 6, из которых 3 описывают поступательное, а 3 – вращательное движения тела. Для определения положения твердого тела необходимо задать:

• Три координаты, фиксирующие положение какой-то точки этого тела в пространстве;
• Два угла для определения направления оси, проходящей через выделенную точку тела;
• Угол поворота тела относительно этой оси.

Таким образом для абсолютно твердого тела число степеней свободы равняется шести. Для каждой степени свободы системы должно быть записано свое уравнение движения, т.е. количество скалярных уравнений движения системы должно совпадать с ее числом степеней свободы.

Итак, для описания механического движения тела (системы тел) необходимо прежде всего задать систему отсчета. Описать механическое движение тела – это означает, что нужно описать механическое движение всех отдельных малых частей этого тела (материальных точек).

9

§2. Кинематика материальной точки

Имеем материальную точку – тело, размерами, формой и внутренним строением которого можно пренебречь.

Для описания механического движения введем СО:

S – линия, которую описывает при своем движении точка – траектория .

- радиус – вектор.

Кинематические уравнения движения - это

уравнения, с помощью которых

описываются изменения положения

материальной точки в пространстве и времени

Вектор перемещения - Вектор, соединяющий начальную (1) движения с конечной (2).

Путь S - расстояние, пройденное точкой вдоль траектории движения от начальной точки (1) до конечной (2), величина скалярная.

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения равен пройденному пути:

Для описания механического движения м.т. введем СО , включающую декартову систему координат и часы, отсчитывающие время.

9

Рассмотрим еще раз рисунок. Возьмем отношение

- вектор средней

скорости перемещения между точками А и В.

Фиксируем положение А, положение В выбираем ближе к точке А и найдем новое отношение

Повторяем эту процедуру, выбираем точку В ближе и ближе к фиксированной точке А.

Предел последовательности указанного отношения дает мгновенную скорость материальной точки в положении А.

Из способа нахождения мгновенной скорости ясно, что она всегда направлена по касательной к траектории.

Вектор мгновенной скорости определяет быстроту изменения радиус-вектора r со временем, т.е. быстроту изменения положения точки в пространстве.

Аналогично определяется и вектор мгновенного ускорения. Выберем два последовательных положения материальной точки А и В . Найдем мгновенную скорость в этих положениях и .

1) Перенесем вектор параллельно самому себе из В в А .

2) Найдем разность векторов и .

Отношение представляет собой вектор среднего ускорения между точками А и В .

3) Будем повторять процедуру, постоянно приближаясь к фиксированной точке А . Предел последовательности таких отношений (предел средних ускорений) – мгновенное ускорение материальной точки в положении А :

В

A

9

Ускорение – Характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю и направлению.

Среднее ускорение – векторная величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло.

Мгновенное ускорение – векторная величина, определяемая первой производной скорости по времени

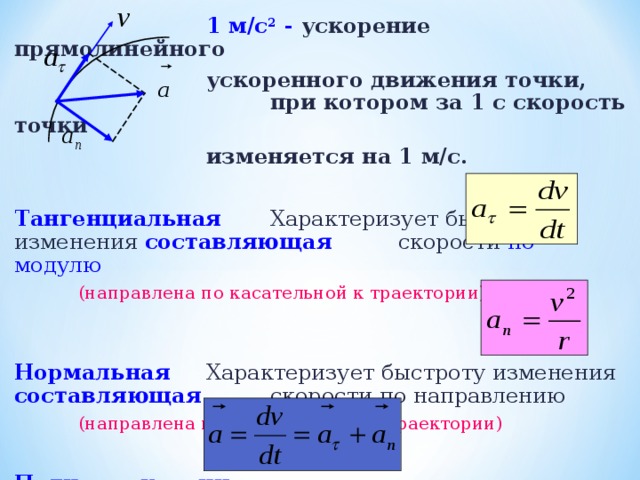
1 м/с 2 - ускорение прямолинейного

ускоренного движения точки, при котором за 1 с скорость точки

изменяется на 1 м/с.

Тангенциальная Характеризует быстроту изменения составляющая скорости по модулю

(направлена по касательной к траектории)

Нормальная Характеризует быстроту изменения составляющая скорости по направлению

(направлена к центру кривизны траектории)

Полное ускорение – геометрическая сумма тангенциальной и нормальной составляющих

• Задача 1. Уравнение движения материальной точки вдоль оси OX имеет вид x = A + Bt + Ct 3 , где А = 2 м, В = 1,5 м/с, С = -0,5 м/с 3 . Найти:

• Координату x, скорость v x , ускорение а x точки в момент времени t = 2 c. Среднюю скорость и среднее ускорение за этот промежуток времени.
• Координату x, скорость v x , ускорение а x точки в момент времени t = 2 c. Среднюю скорость и среднее ускорение за этот промежуток времени.
• Координату x, скорость v x , ускорение а x точки в момент времени t = 2 c.
• Среднюю скорость и среднее ускорение за этот промежуток времени.

Решение:

• Решение:
• Решение:

Средняя скорость – отношение всего пути, пройденного телом ко времени. Найдем значение времени, когда тело изменило направление движения на противоположное. В этот момент времени мгновенная скорость равна 0.

Определим путь за время 2 с:

• Средняя скорость – отношение всего пути, пройденного телом ко времени. Найдем значение времени, когда тело изменило направление движения на противоположное. В этот момент времени мгновенная скорость равна 0. Определим путь за время 2 с:
• Средняя скорость – отношение всего пути, пройденного телом ко времени. Найдем значение времени, когда тело изменило направление движения на противоположное. В этот момент времени мгновенная скорость равна 0. Определим путь за время 2 с:

Среднее ускорение –

- скорость в момент времени t 2 = 2 c.

- скорость в момент времени t 1 = 0 c.

• Среднее ускорение – - скорость в момент времени t 2 = 2 c. - скорость в момент времени t 1 = 0 c.
• Среднее ускорение – - скорость в момент времени t 2 = 2 c. - скорость в момент времени t 1 = 0 c.

Задача 2 . Электрон движется в некоторой системе

отсчета из начального положения, определяемого

радиус-вектором , где x 0 = 3 м , z 0 = 1 м

с начальной скоростью , где v 0 y = 2 м/с и

ускорением , где А = 12 м/с 2 , В = 8 м/с 2 .

Найти:

• Координату z электрона в момент времени
• Координату z электрона в момент времени
• Координату z электрона в момент времени

t = 0,5 с.

2. Скорость электрона в момент времени

t = 1 с,

3. Угол между радиусом–вектором и вектором скорости в момент времени

t = 0 с.

• t = 0,5 с. 2. Скорость электрона в момент времени t = 1 с, 3. Угол между радиусом–вектором и вектором скорости в момент времени t = 0 с.
• t = 0,5 с. 2. Скорость электрона в момент времени t = 1 с, 3. Угол между радиусом–вектором и вектором скорости в момент времени t = 0 с.

Решение:

2) Модуль скорости, если ускорение зависит от времени определяется:

Модуль ускорения:

Кинематические уравнения скоростей:

• Решение: 2) Модуль скорости, если ускорение зависит от времени определяется: Модуль ускорения: Кинематические уравнения скоростей:
• Решение: 2) Модуль скорости, если ускорение зависит от времени определяется: Модуль ускорения: Кинематические уравнения скоростей:

Учитываем начальные условия м/с:

Вектор модуля скорости:

(м/с)

Модуль скорости в момент времени t = 1 с:

м/с;

1) Координата z электрона в момент времени t = 0,5 с:

• Учитываем начальные условия м/с: Вектор модуля скорости: (м/с) Модуль скорости в момент времени t = 1 с: м/с; 1) Координата z электрона в момент времени t = 0,5 с:
• Учитываем начальные условия м/с: Вектор модуля скорости: (м/с) Модуль скорости в момент времени t = 1 с: м/с; 1) Координата z электрона в момент времени t = 0,5 с:

3) Угол между радиусом–вектором и вектором скорости в момент t = 0 с определим, используя скалярное произведение этих векторов:

Следовательно,

• 3) Угол между радиусом–вектором и вектором скорости в момент t = 0 с определим, используя скалярное произведение этих векторов: Следовательно,
• 3) Угол между радиусом–вектором и вектором скорости в момент t = 0 с определим, используя скалярное произведение этих векторов: Следовательно,

Задача 3 . Автомобиль движется по закруглению шоссе, имеющему радиус кривизны . Уравнение движения автомобиля , где А = 10 м, В = 10 м/с, С = -0,5 м/с 2 .

Найти:

• Скорость автомобиля v , его тангенциальное ускорение a  ,
• Скорость автомобиля v , его тангенциальное ускорение a  ,
• Скорость автомобиля v , его тангенциальное ускорение a  ,

нормальное a n  и полное ускорения a  

в момент времени t = 5 с.

2. Длину пути и модуль перемещения автомобиля за интервал времени  = 10 с, отсчитанный с момента начала движения.

• нормальное a n  и полное ускорения a   в момент времени t = 5 с. 2. Длину пути и модуль перемещения автомобиля за интервал времени  = 10 с, отсчитанный с момента начала движения.
• нормальное a n  и полное ускорения a   в момент времени t = 5 с. 2. Длину пути и модуль перемещения автомобиля за интервал времени  = 10 с, отсчитанный с момента начала движения.

Решение:

1) Мгновенная скорость – первая производная от координаты по времени:

Тангенциальное ускорение найдем, взяв первую производную от скорости по времени:

Нормальное ускорение:

Полное ускорение

• Решение: 1) Мгновенная скорость – первая производная от координаты по времени: Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: Нормальное ускорение: Полное ускорение
• Решение: 1) Мгновенная скорость – первая производная от координаты по времени: Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: Нормальное ускорение: Полное ускорение

2) Путь, пройденный автомобилем в одном направлении, равен изменению координаты:

Модуль перемещения:

• 2) Путь, пройденный автомобилем в одном направлении, равен изменению координаты: Модуль перемещения:
• 2) Путь, пройденный автомобилем в одном направлении, равен изменению координаты: Модуль перемещения:

Задача 1. Первую четверть пути автомобиль двигался со скорость 60 км/ч, остальной путь – со скоростью 20 км/ч. Найдите среднюю скорость автомобиля.

Решение: Средняя скорость

Полное время движения равно сумме времен движения на отдельных участках:

Подставляем:

Получим:

Задача 2. Из окна, находящегося на высоте h 0 = 7,5 м, бросают камень под углом 45 0 к горизонту. Камень упал на расстоянии s = 15 м от стены дома. С какой скоростью v 0 был брошен камень?

Решение:

Запишем зависимость координат камня от времени

Учтем, что в момент падения

Из первого уравнения выразим время

Подставим во второе уравнение

Задача 3. Камень брошен вертикально вверх со скоростью v 0 = 50 м/с. Через сколько секунд его скорость будет равна v = 30 м/с и направлена вниз.

Решение: Формулы равноускоренного движения действуют все время равноускоренного движения.

• Направим ось OY вертикально вверх.
• Воспользуемся формулой:
• В данном случае

Получаем:

Проверка: за время t 1 = v 0 /g = 5 c – поднимается вверх, а затем за t 2 = t – t 1 = 3 с набирает скорость v = g t 2 = 30 м/с .